证明:假设是有理数,
那么存在两个互质的正整数、
, 使得
, 于是
,
∴ ▲
∵是偶数,可得
是偶数.
∵只有偶数的平方才是偶数,∴也是偶数.
∴可设 , 代入,得 ▲ .可得 ▲
∴ ▲ .这样,和
都是偶数,不互质,这与假设
,
互质矛盾.
这个矛盾说明,不能写成分数的形式,即
不是有理数.
将下列选项依次填入材料中的画线处,正确的顺序是.(填上序号)
①; ②
; ③
是偶数; ④
.

游戏规则a.两人依次在网格中画线段,线段的起点和终点均为格点; b.新画线段的起点为前一条线段的终点,且与任意已画出线段不能有其它公共点; c.已画出线段的所有端点中,任意三个端点不能在同一条直线上; d.当某人无法画出新的线段时,则另一人获胜. |
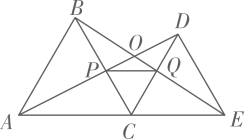
如图2,甲先画出线段 , 乙随后画出线段
.若这局游戏继续进行下去,最终的获胜者是.(填“甲”,“乙”或“不确定”).

![]()
甲、乙两人轮流从中取走小球,规则如下:
①每人首次取球时,只能取走2个或3个球;后续每次可取走1个,2个或3个球;
②取走2个或3个球时,必须从相邻的格子中取走;
③最后一个将球取完的人获胜.

车床编号 | 甲、乙 | 乙、丙 | 丙、丁 | 丁、戊 | 甲、戊 |
所需时间(h) | 13 | 9 | 10 | 12 | 8 |
则加工W型零件最快的一台车床的编号是 .
已知:如图, ,
, 求证:
.

证明:∵(已知)
且( ),
∴(等量代换).
∴ ▲ (同位角相等,两直线平行).
∴( ).
∵(已知),
∴( ).
∴ ▲ (两直线平行,内错角相等).
∴(等量代换).
勾股定理,是指直角三角形的两条直角边的平方和等于斜边的平方.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派.
中国古代称直角三角形为勾股形(直角边中较小者为勾,另一长直角边为股,斜边为弦),周朝时期的商高提出了“勾三股四弦五”的特例,所以我国称这个定理为勾股定理,也有人称商高定理.
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。下面是小明搜集到的勾股定理的一种证明方法(不完整).
如图,在中,
,
,
,
.
求证: .
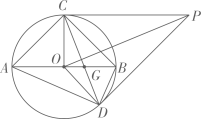
证明:作出的外接圆O.延长
到点D,使得
. 连接
, 交
于点E.延长
与
的延长线交于点M.连接
, 延长
与
交于点N
∵ , ∴
,
为
的直径.
∴ . (依据1)
∴ ,
…

学习任务:
∵“ ∴当“ |
现在,设是个四位数,其个位、十位、百位、千位上的数字分别是d,c,b,a,请你借鉴小明的思路,证明:若“
”能被3整除,则
能被3整除;
①互补三角形一定不全等.命题
②互补三角形的面积相等.命题
求证:;

材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末n位能被 整除的数,本身必能被
整除,反过来,末n位不能被
整除的数,本身也不可能被
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
,
为整数,
能被25整除
,
不为整数,
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.

我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ= QR = RS,(这个条件很重要哦!)勾 尺的一边 MN 满足M, N, Q三点共线(所以PQ ⊥ MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE //BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP:
请完成第三步操作,图中∠ABC的三等分线是射线、.
∵,BQ⊥PR,
∴BP= BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠RBQ=∠PBQ,
∵PT⊥BC,PQ⊥BQ,PT=PQ,
∴∠= ∠. (角的内部到角的两边距离相等的点在角的平分线上)
∴∠ == ∠= ∠
∠ABS= ∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV =
∠ABC(无需写画法,保留画图痕迹即可)