一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
-
-
-
4.
(2024高二上·重庆市期末)
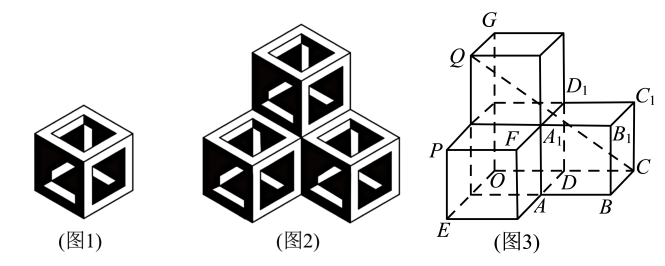
布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达·芬奇方砖拼成图2的组合,这个组合再转换成图3所示的空间几何体.若图3中每个正方体的棱长为1,则直线
CQ与平面

所成角的正弦值为( )
-
-
6.
(2024高二上·重庆市期末)
折纸是一种以纸张折成各种不同形状的艺术活动,折纸大约起游于公元1世纪或者2世纪时的中国,折纸与自然科学结合在一起,不仅成为建筑学院的教具,还发展出了折纸几何学成为现代几何学的一个分支.如图,现有一半径为4的圆纸片(
A为圆心,
B为圆内的一定点),且

, 如图将圆折起一角,使圆周正好过点
B , 把纸片展开,并留下一条折痕,折痕上到
A ,
B两点距离之和最小的点为
P , 如此往复,就能得到越来越多的折痕,设
P点的轨迹为曲线
C.在
C上任取一点
M , 则△
MAB面积的最大值是( )

A . 2
B . 3
C .  D .
D . 
-
7.
(2024高二上·重庆市期末)
已知椭圆的方程为

,上顶点为

,左顶点为

,设

为椭圆上一点,则

面积的最大值为

.若已知

,点

为椭圆上任意一点,则

的最小值为( )
A . 2
B .  C . 3
D .
C . 3
D . 
-
A . 9
B . 10
C . 14
D . 
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求的。全部选对的得5分,部分选对的得2分,有选错的得2分。
三、填空题:本题共4小题,每小题5分,共20分。
-
-
-
15.
(2024高二上·重庆市期末)
古希腊数学家阿波罗尼斯(
Apollonius of Perga , 约公元前262~190年)发现:平面上两定点
A ,
B , 则满足

的动点
M的轨迹是一个圆,后人称这个圆为阿波罗尼斯圆,简称阿氏圆.在直角坐标系
xOy中,已知

, 动点
M满足

, 则

面积的最大值为
.
-
16.
(2024高二上·重庆市期末)
如图抛物线

的顶点为
A , 焦点为
F , 准线为

, 焦准距为4;抛物线

的顶点为
B , 焦点也为
F , 准线为

, 焦准距为6.

和

交于
P、
Q两点,分别过
P、
Q作直线与两准线垂直,垂足分别为
M、
N、
S、
T , 过
F的直线与封闭曲线
APBQ交于
C、
D两点,则下列说法正确的是
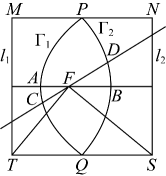
① ;②四边形MNST的面积为
;②四边形MNST的面积为 ;③
;③ ;④
;④ 的取值范围为
的取值范围为 .
.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
17.
(2024高二上·重庆市期末)
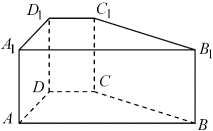
如图,已知直四棱柱

中,

, 底面

是直角梯形,

为直角,
AB∥
CD ,

,

,

, 请建立适当空间直角坐标系,并求各个点的坐标.
-
-
19.
(2024高二上·重庆市期末)
已知抛物线

的焦点为

是抛物线上一点且三角形
MOF的面积为

(其中
O为坐标原点),不过点
M的直线
l与抛物线
C交于
P ,
Q两点,且以
PQ为直径的圆经过点
M , 过点
M作

交
PQ于点
N.
-
-
(2)
求证直线PQ恒过定点,并求出点N的轨迹方程.
-
-
(1)
求证:

;
-
(2)
求直线

与平面

所成角的正弦值;
-
(3)
求点
D到平面

的距离.

-
-
(1)
证明:

;
-
(2)
求二面角

的余弦值.
-
-
-
(2)
设直线

与椭圆交于

两点,且以

为对角线的菱形的一个顶点为

, 求

面积的最大值及此时直线

的方程.


;②四边形MNST的面积为
;③
;④
的取值范围为
.
