2023-2024学年湘教版初中数学九年级下册 2.4 过不...

更新时间：2024-01-27 浏览次数：35 类型：同步测试

一、选择题

1. (2024九上·杭州月考) 已知在Rt△ABC中，∠C=90°，AC=5，BC=12，则△ABC的外接圆直径为（）

A . 5 B . 12 C . 13 D . 6.5

答案解析收藏纠错 + 选题
2. (2023九上·南宁期中) 在平面直角坐标系中，已知点A（0，1），B（0，﹣5），若在x轴正半轴上有一点C，使∠ACB＝30°，则点C的横坐标是（）

A . 3 $\text{[math]}$ 4 $\text{[math]}$ B . 12 C . 6+3 $\text{[math]}$ D . 6 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·景县期中) 如图，在平面直角坐标系中，点A、B、C的坐标为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 外接圆的圆心坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·石家庄期中) 已知锐角 $\text{[math]}$ 中，O是 $\text{[math]}$ 的中点，甲、乙二人想在 $\text{[math]}$ 上找一点P ，使得 $\text{[math]}$ 的外心为点O ，其做法如图．对于甲、乙二人的做法，正确的是（）

A . 两人都正确. B . 只有甲正确 C . 只有乙正确 D . 两人都不正确

答案解析收藏纠错 + 选题
5. (2023九上·绍兴期中) 如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述不正确的是（）

A . O是△AEB的外心，O不是△AED的外心 B . O是△BEC的外心，O不是△BCD的外心 C . O是△AEC的外心，O不是△BCD的外心 D . O是△ADB的外心，O不是△ADC的外心

答案解析收藏纠错 + 选题
6. (2023九上·余姚期中) 如图，点A，B的坐标分别为A（2，0），B（0，2），点C为坐标平面内一点，BC＝1，点M为线段AC的中点，连接OM，则OM的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023七下·青岛期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别作 $\text{[math]}$ ， $\text{[math]}$ 两边的垂直平分线 $\text{[math]}$ 、 $\text{[math]}$ ，垂足分别是点M、N，以下说法：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④点P到点B和点C的距离相等．其中正确的是（）

A . ①②③ B . ①②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
8. (2023·深圳模拟) 如图，直线l： $\text{[math]}$ 分别与x轴、y轴交于点A、B ．点P为直线l在第一象限的点．作△POB的外接圆 $\text{[math]}$ ，延长OC交 $\text{[math]}$ 于点D ，当△POD的面积最小时，则 $\text{[math]}$ 的半径长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题

二、填空题

9. (2023九上·香坊月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 的外接圆的半径为．

答案解析收藏纠错 + 选题
10. 如图，⊙O是△ABC的外接圆，BC是⊙O的直径，AB=AC．∠ABC的平分线交AC于点D，交⊙O于点E，连结CE．若CE= $\text{[math]}$ ，则BD的长为

答案解析收藏纠错 + 选题
11. 如图，将△ABC放在每个小正方形的边长为1的网格中，点A，B，C均落在格点上．用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是

答案解析收藏纠错 + 选题
12. (2023九上·瑞安期中) 如图，已知半圆O ， OB＝ $\text{[math]}$ ．点D在半圆上，AD＝10，在 $\text{[math]}$ 取点C ，连结AC ，作DH⊥AC于点H ，连结BH ，则BH的最小值等于．

答案解析收藏纠错 + 选题
13. (2023·宁波模拟) 如图，在等腰三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ，将该纸片翻折，使得点C落在边 $\text{[math]}$ 的F处，折痕为 $\text{[math]}$ ， D，E分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 的面积为.

答案解析收藏纠错 + 选题

三、解答题

14. (2021九上·杭州期中) 如图，已知抛物线y＝-x²+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C，⊙M是△ABC的外接圆．若抛物线的顶点D的坐标为（1，4）．
1. （1）求抛物线的解析式，及A、B、C三点的坐标；
2. （2）求⊙M的半径和圆心M的坐标；
3. （3）如图2，在x轴上有点P（7，0），试在直线BC上找点Q，使B、Q、P三点构成的三角形与△ABC相似．若存在，请直接写出点坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
15.
如图，已知△ABC内接于⊙O，AD、AE分别平分∠BAC和△BAC的外角∠BAF，且分别交圆于点D、F，连接DE，CD，DE与BC相交于点G．
（1）求证：DE是△ABC的外接圆的直径；
（2）设OG=3，CD= $\text{[math]}$ ，求⊙O的半径．

答案解析收藏纠错 + 选题

四、综合题

16. (2023·宜城模拟) 已知菱形ABCD的边长为4．∠ADC=60°，等边△AEF两边分别交边DC，CB于点E，F．
1. （1）特殊发现：如图1，若点E，F分别是边DC，CB的中点．求证：菱形ABCD对角线AC，BD的交点O即为等边△AEF的外心；
2. （2）若点E，F始终分别在边DC，CB上移动，等边△AEF的外心为点P．
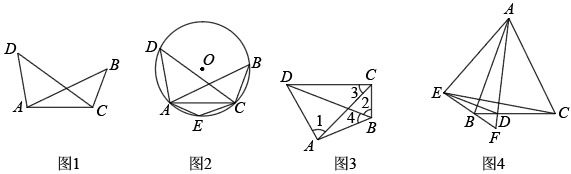
  ①猜想验证：如图2．猜想△AEF的外心P落在哪条直线上，并加以证明；
  
  ②学以致用：如图3，当△AEF的面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2023九上·鄞州期末) 综合与实践
“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题：
如图1，在线段AC同侧有两点B，D，连接 $\text{[math]}$ ，如果 $\text{[math]}$ ，那么A，B，C，D四点在同一个圆上.
探究展示：求证：点A，B，C，D四点在同一个圆上
如图2，作经过点A，C，D的 $\text{[math]}$ ，在劣弧 $\text{[math]}$ 上取一点E（不与A，C重合），连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .
1. （1）请完善探究展示
2. （2）如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，则∠4的度数为.
3. （3）拓展探究：如图4，已知 $\text{[math]}$ 是等腰三角形， $\text{[math]}$ ，点D在 $\text{[math]}$ 上（不与 $\text{[math]}$ 的中点重合），连接 $\text{[math]}$ .作点C关于 $\text{[math]}$ 的对称点E，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于F，连接 $\text{[math]}$ .
  ①求证：A，D，B，E四点共圆；
  ②若 $\text{[math]}$ ， $\text{[math]}$ 的值是否会发生变化，若不变化，求出其值；若变化，请说明理由
答案解析收藏纠错 + 选题