 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B . 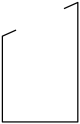 C .
C . 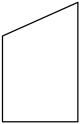 D .
D . 


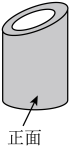
①如图1,货车匀速通过隧道(隧道长大于货车长),货车在隧道内的长度y与从车头进入隧道至车尾离开隧道的时间x;
②如图2,实线是王大爷从家出发匀速散步行走的路线(圆心O表示王大爷家的位置),他离家的距离y与散步的时间x;
③如图3,往一个圆柱形空杯中匀速倒水,倒满后停止,一段时间后,再匀速倒出杯中的水,杯中水的体积y与所用时间x
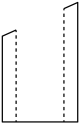
其中,变量y与x之间的函数关系大致符合图4的是( )

投壶次数n | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
投中次数m | 28 | 46 | 72 | 104 | 125 | 153 | 200 | 250 |
投中频率 | 0.56 | 0.46 | 0.48 | 0.52 | 0.50 | 0.51 | 0.50 | 0.50 |
根据以上数据,估计这组游戏参与者投中的概率约为(结果精确到0.1).


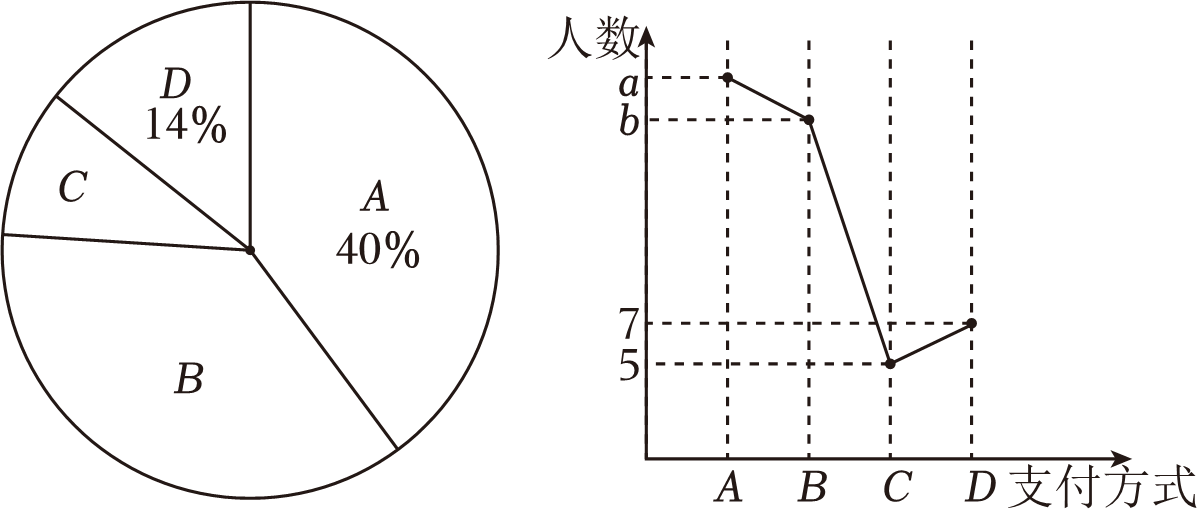
根据统计图表中的信息,解答下列问题:
①以O为位似中心,将△ABC缩小为原来的![]() , 得到△A1B1C1 , 请在y轴右侧画出△A1B1C1;
, 得到△A1B1C1 , 请在y轴右侧画出△A1B1C1;
②△ABC的面积为 ▲ ;
③在网格中找一点D,使得△BCD向是以BC为底边的等腰直角三角,则点D的坐标为 ▲ .


请从中选择一个能证明四边形EBCD是菱形的条件,并写出证明过程;
如图1,某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为am.

【问题提出】
小组同学提出这样一个问题:若a=10,能否围出矩形地块?
小颖尝试从“函数图象”的角度解决这个问题:
设AB为xm,BC为ym.由矩形地块面积为8m2 , 得到xy=8,满足条件的(x,y)可看成是反比例函数y=的图象在第一象限内点的坐标;木栏总长为10m,得到2x+y=10,满足条件的(x,y)可看成一次函数y=﹣2x+10的图象在第一象限内点的坐标,同时满足这两个条件的(x,y)就可以看成两个函数图象交点的坐标.
如图2,反比例函数y=(x>0)的图象与直线l1:y=﹣2x+10的交点坐标为(1,8)和,因此,木栏总长为10m时,能围出矩形地块,分别为:AB=1m,BC=8m;或AB=m,BC=m.
根据小颖的分析思路,完成上面的填空;
若a=6,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由;
当木栏总长为am时,小颖建立了一次函数y=﹣2x+a.发现直线y=﹣2x+a可以看成是直线y=﹣2x通过平移得到的,在平移过程中,当过点(2,4)时,直线y=﹣2x+a与反比例函数y=(x>0)的图象有唯一交点.
请在图2中画出直线y=﹣2x+a过点(2,4)时的图象,并求出a的值;
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=﹣2x+a与y=图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且AB和BC的长均不小于1m,请直接写出a的取值范围.