

小题1:如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是,长是,面积是 (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式 (用式子表达).
解: ,
①
②
.
解:∵x2-2xy+2y2-8y+16=0,
∴(x2-2xy+y2)+(y2-8y+16)=0
∴(x-y)2+(y-4)2=0,
∴(x-y)2=0,(y-4)2=0,
∴y=4,x=4.
根据你的观察,探究下面的问题:
已知a、b满足a2+b2-4a-6b+13=0.求a、b的值.
解:∵x2-2xy+2y2-8y+16=0,∴(x2-2xy+y2)+(y2-8y+16)=0,∴(x-y)2+(y-4)2=0,∴(x-y)2=0,(y-4)2=0,∴y=4,x=4.
根据你的观察,探究下面的问题:
已知△ABC的三边长a、b、c都是正整数,且满足a2+b2-4a-6b+13=0.求△ABC的边c的值.
(a﹣b)(a+b)=;
(a﹣b)(a2+ab+b2)=;
(a﹣b)(a3+a2b+ab2+b3)=;
…
(a﹣b)(a2022+a2021b+…+ab2021+b2022)=.
【数学探究】
① ,
② ,
③;

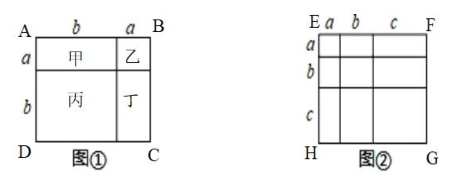
探究:如图①,用含a,b的式子完成以下题目中的(2)和(3):(1)正方形ABCD的边长为 , 因为正方形的面积等于正方形边长的平方,所以正方形ABCD的面积可以表示为
.
如图1是两直角边长分别为 ,
的直角三角形,如果用四个与图1完全一样的直角三角形可以拼成如图2和图3的几何图形,其中图2和图3的四边形
、四边形
都是正方形、请你根据几何图形部分与整体的关系完成下列各题
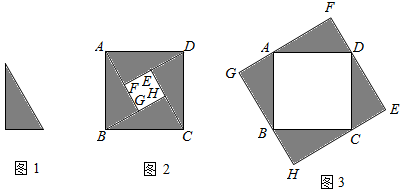
图2中正方形的面积:.
图3中正方形的面积:.
①已知: ,
, 求:
的值;
②已知: ,
, 求:
的值.
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
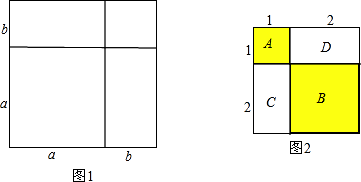
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1:
这个图形的面积可以表示成:
(a+b)2或 a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
类比解决:
①请你类比上述方法,利用图形的几何意义证明平方差公式.(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明:13+23=32?
如图2,A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23
而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
尝试解决:
②请你类比上述推导过程,利用图形的几何意义确定:13+23+33= ▲ . (要求写出结论并构造图形写出推证过程).
问题拓广:
③请用上面的表示几何图形面积的方法探究:13+23+33+…+n3= ▲ . (直接写出结论即可,不必写出解题过程)
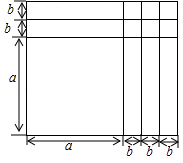
活动主题:探究图形面积与代数式之间的关系
活动资源:提供长度不同的两种木棒各根
如图

入项任务:运用以上根木棒
不折断
摆成长方形或正方形,且木棒全部用完
选取同学们的甲、乙、丙、丁四种不同的摆法
如图
进行研究.

问题探究过程
请观察以上所有图形,并研究不同2种或2种以上摆法的图形面积之间关系,你发现哪些结论?
例如:小明发现:甲摆法的面积是乙摆法总面积的2倍.
小张发现:丁摆法的总面积大于乙摆法的总面积.
聪明的你,能提出不同于小明和小张的更创新更有意义问题吗?
你的发现是;请用简洁的语言描述
请用代数式表示你的发现设两种木棒的长度分别为
,
其中
, 四种图形面积分别为
,
,
,
.
例如:小明的结论是 .
小张的结论是 ,
你的结论是:;
请用所学的数学知识证明你的结论.
例如:小明的证明方法如下.
证: ,
,
,
你的证明:;
把甲摆法围成大长方形纸片沿虚线剪成四个全等的小长方形,请用四个小长方形拼摆出边长为的正方形,画出示意图,并用等式表达示意图中的各图形面积之间的关系.
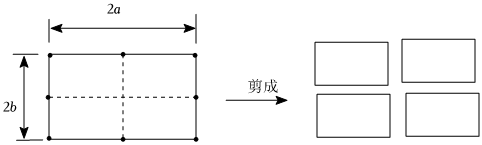
你的示意图:;
你的关系式:.
根据以上的研究结论,请解决数学问题,若 ,
, 求
的值.
你的解答:.
制作一个体积为 , 底面为正方形的长方体包装盒,当底面边长为多少时,需要的材料最省(底面边长不超过3
, 且不考虑接缝).

某小组经讨论得出:材料最省,就是尽可能使得长方体的表面积最小.
下面是他们的探究过程,请补充完整:
得到y与x的关系式:();
x/ | … | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
… | 80.5 | 42.0 | 31.2 | ① | 28.5 | 31.3 |

长方体包装盒的底面边长约为时,需要的材料最省.