2023-2024学年初中数学人教版七年级下学期第七章平...

更新时间：2024-03-19 浏览次数：63 类型：单元试卷

一、选择题

1. (2017七下·路北期末) 在平面直角坐标系中，点P（﹣5，0）在（）

A . 第二象限 B . x轴上 C . 第四象限 D . y轴上

答案解析收藏纠错 + 选题
2. (2020七下·钦州期末) 在平面直角坐标系中，已知 $\text{[math]}$ ，则点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距离为（）

A . -2 B . 2 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·绥阳月考) 如果 $\text{[math]}$ ，那么点P $\text{[math]}$ 所在象限为（）

A . 第二象限 B . 第四象限 C . 第一或第三象限 D . 第二或第四象限

答案解析收藏纠错 + 选题
4. (2023七下·巩义期末) 已知点Q的坐标为 $\text{[math]}$ ，点P的坐标为 $\text{[math]}$ ，若直线 $\text{[math]}$ 轴，则点P的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·凉州期中) 已知点 $\text{[math]}$ ，若直线 $\text{[math]}$ 与x轴平行，则N点坐标可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·良庆期末) 某气象台为了预报台风，首先需要确定台风中心的位置，则下列说法能确定台风中心位置的是（）

A . 北纬 $\text{[math]}$ B . 距气象台 $\text{[math]}$ 海里 C . 北纬 $\text{[math]}$ ，东经 $\text{[math]}$ D . 北海市附近

答案解析收藏纠错 + 选题
7. (2023七下·罗源期末) 在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ，则线段 $\text{[math]}$ 上任意一点的坐标可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·台江期末) 某学校的平面示意图如图所示，如果医院所在位置的坐标为 $\text{[math]}$ ，则 $\text{[math]}$ 所在的位置是（）

A . 医院 B . 学校 C . 汽车站 D . 水果店

答案解析收藏纠错 + 选题
9. (2023七下·江南期末) 如图，小手盖住的点的坐标可能是（　　）．

A . （﹣3，4）； B . （5，2） C . （﹣3，﹣6）； D . （6，﹣4）．

答案解析收藏纠错 + 选题
10. (2023七下·良庆期末) 如果点 $\text{[math]}$ 的坐标满足 $\text{[math]}$ ，那么称点 $\text{[math]}$ 为“美丽点”，若某个“美丽点” $\text{[math]}$ 到 $\text{[math]}$ 轴的距离为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023七下·江汉期末) 若点 $\text{[math]}$ 在x轴上，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023七下·良庆期末) 如图所示，若“兵”的位置是 $\text{[math]}$ ， “炮”的位置是 $\text{[math]}$ ，则“将”的位置可以表示为．

答案解析收藏纠错 + 选题
13. (2024八上·杭州月考) 在平面直角坐标系中，若点M（1，x）与点N（1，3）之间的距离是5，则x的值是．

答案解析收藏纠错 + 选题
14. (2024七下·黄石期末) 已知两点 $\text{[math]}$ ， $\text{[math]}$ 的距离为4，且直线 $\text{[math]}$ 轴，则 $\text{[math]}$ 的算术平方根为；

答案解析收藏纠错 + 选题
15. (2024七下·凉州期中) 在平面直角坐标系中，点 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ，若在平面直角坐标中存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，且 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题

三、解答题

16. (2024七下·凉州期中) 已知在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ．
1. （1）若点A在 $\text{[math]}$ 轴上，求出点A的坐标；
2. （2）若点A到 $\text{[math]}$ 轴的距离为 $\text{[math]}$ ，求出点A的坐标．
答案解析收藏纠错 + 选题
17. (2023七下·临翔期末) 已知点 $\text{[math]}$ ，解答下列问题：
1. （1）若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，且 $\text{[math]}$ 轴，求 $\text{[math]}$ 的值；
2. （2）若点 $\text{[math]}$ 在第四象限，且 $\text{[math]}$ 是整数，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
18. (2023七下·楚雄期末) 已知点 $\text{[math]}$ ，根据条件，求点A的坐标．
1. （1）点A的横坐标是纵坐标的2倍．
2. （2）点A在过点 $\text{[math]}$ 且与 $\text{[math]}$ 轴平行的直线上．
答案解析收藏纠错 + 选题

四、实践探究题

19. (2023八上·梧州期中) 综合与实践：
1. （1）问题背景：
  已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．在平面直角坐标系中描出这几个点，并分别找到线段 $\text{[math]}$ 和 $\text{[math]}$ 中点 $\text{[math]}$ 、 $\text{[math]}$ ，然后写出它们的坐标，则 $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ．
2. （2）探究发现：
  结合上述计算结果，你能发现若线段的两个端点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，则线段的中点坐标为．
3. （3）拓展应用：
  利用上述规律解决下列问题：已知三点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，第四个点 $\text{[math]}$ 与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．
答案解析收藏纠错 + 选题
20. (2023八上·天桥月考) 老师布置了一项编题作业给小亮，小颖和小明的学习小组：结合图象创设情景，加入适当的条件，设计一道数学问题，并作出合理的解释。以下是老师参与下的学习小组活动片段.
[观察图象]
如图，是老师在平面直角坐标系中画出的图象，请同学们结合图象创设背景。
[创设背景]
小颖说：可以创设这样的背影：一辆货车从甲地行驶到乙地去拉货，到达乙地后旋即返回，这里横坐标表示行驶的时间，单位是小时，纵坐标表示货车与甲地的距离，单位是千米。
小亮说：显然去时的速度快于返回的速度，可设去乙地的速度为60km/h，返回甲地的速度为30km/h.
小明说：还应该给出条件，甲、乙两地间的距离为120千米。
老师说：非常好，这样就可以试着提出问题了。
[提出问题]
小颖说：可以求货车从甲地去乙地的时间是多少。
小亮说：可以问A、B两地的坐标是多少。
小明说：可以问货车何时距离甲地30km。
老师说：大家的想法真好，就按大家的设计，下面可以概括出题了。
请结合以上对话，回答问题：
1. （1）货车从甲地去乙地时间为h.
2. （2）请求出图中A、B两点的坐标.
3. （3）当货车距离甲地30km时，行驶的时间是多少？
答案解析收藏纠错 + 选题
21. (2023七下·南宁期末) 阅读材料回答问题
在平面直角坐标系中，定义，点P沿着水平和竖直方向运动到达点Q的最短路径的长度为P ， Q两点之间的“横纵距离”.如图所示，点A的坐标为 $\text{[math]}$ ，则A ， O两点的“横纵距离”为5．
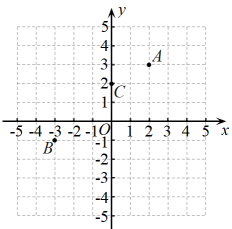
解决问题
1. （1）已知点B的坐标为 $\text{[math]}$ ，则B ， O两点的“横纵距离”为；A ， B两点的“横纵距离”为；
2. （2）已知点C的坐标为 $\text{[math]}$ ，写出两个与点C的“横纵距离”为3的点的坐标．
3. （3）拓展延伸
  已知D ， O两点的“横纵距离”为5；D ， C两点的“横纵距离”为3.请写出满足条件的点D的纵坐标的取值范围．
答案解析收藏纠错 + 选题

五、综合题

22. (2023七下·杜尔伯特月考) 如图，这是某校的平面示意图，如以正东为x轴正方向，正北为y轴正方向建立平面直角坐标系后，得到初中楼的坐标是 $\text{[math]}$ ，实验楼的坐标是 $\text{[math]}$ ．
1. （1）坐标原点应为的位置．
2. （2）在图中画出此平面直角坐标系；
3. （3）校门在第象限；图书馆的坐标是；分布在第一象限的是．
答案解析收藏纠错 + 选题
23. (2023七下·平泉期末) 已知点 $\text{[math]}$
1. （1）当点 $\text{[math]}$ 在 $\text{[math]}$ 轴上时，求点 $\text{[math]}$ 坐标及 $\text{[math]}$ 的面积；
2. （2）当 $\text{[math]}$ 轴时：
  ①求 $\text{[math]}$ 两点之间的距离；
  ②直接比较 $\text{[math]}$ ▲ $\text{[math]}$ （填“>”或“<”或“=”）
3. （3）点 $\text{[math]}$ 不可能在第象限．
答案解析收藏纠错 + 选题