2023-2024学年初中数学人教版八年级下学期第十八章 ...

更新时间：2024-03-19 浏览次数：452 类型：单元试卷

一、选择题

1. 下列命题中，属于假命题的是（）

A . 菱形的面积等于两条对角线乘积的一半 B . 矩形的对角线相等 C . 对角线互相垂直的平行四边形是矩形 D . 对角线相等的菱形是正方形

答案解析收藏纠错 + 选题
2. 已知四边形ABCD是菱形，则下列结论中，不一定正确的是（）

A . ∠A=∠B=∠C=∠D B . AB=BC=CD=DA C . AC⊥BD D . AC平分∠BAD和∠BCD

答案解析收藏纠错 + 选题
3. 如图，D，E分别是△ABC的边BA，BC的中点.若AC=3，则 DE 的长为（）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 如图，在△ABC中，D是AB 的中点，E，F在AC 上，且AE=EF，BC=CF.若∠A=25°，∠ADE=10°，则∠ABC的度数为（）

A . 35° B . 40° C . 45° D . 50°

答案解析收藏纠错 + 选题
5. 如图，在▱ABCD 中，AC 与 BD 相交于点O，∠ODA=90°，OA=6，OB=2，则AD的长是（）

A . 6 B . 4 $\text{[math]}$ C . 4 D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
6. 如图，在矩形ABCD中，AO=5，CD=6，则AD的长为（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
7. 已知四边形 ABCD 是平行四边形，有下列条件：①AB=BC；②∠ABC=90°；③∠ABD=∠CBD；④AC⊥BD. 从中选一个条件作为补充，能使□ABCD变为菱形的是（）

A . ① B . ①③ C . ②④ D . ①③④

答案解析收藏纠错 + 选题
8. 如图，□ABCD的两条对角线相交于点O.若AC=4，BD=5，BC=3，则△BOC的周长为（）

A . 6 B . 7.5 C . 9 D . 12

答案解析收藏纠错 + 选题
9. 依据所标数据，下列四边形一定为平行四边形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. 如图，在正方形 ABCD中，E是AC 上的一点，且 AB=AE，则∠EBC的度数为（）

A . 37.5° B . 30° C . 22.5° D . 12.5°

答案解析收藏纠错 + 选题

二、填空题

11. 在 $\text{[math]}$ ABCD中，已知AB=15，AC=13，BC边上的高等于12，则 $\text{[math]}$ ABCD的周长是 .

答案解析收藏纠错 + 选题
12. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上， EF⊥AB，OG∥EF，AD=10，EF=4，则BG的长为.

答案解析收藏纠错 + 选题
13. 如图，在矩形 ABCD的边AD 上找一点 P，使点 P 到B，C两点的距离之和最短，则点 P 的位置应该在.

答案解析收藏纠错 + 选题
14. 如图，在菱形ABCD中，AB=10cm，AC=16cm，E，F分别是CD和BC的中点，连结EP并延长与AB的延长线相交于点G，则EG的长度为cm

答案解析收藏纠错 + 选题
15. (2023八下·兴仁月考) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点E，交 $\text{[math]}$ 的延长线于点F，则 $\text{[math]}$ cm．

答案解析收藏纠错 + 选题

三、作图题

16. 如图所示为两张大小完全相同的6×6方格纸，每个小方格都是边长为1的正方形，小方格的顶点叫做格点，以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形，按下列要求画出拼图后的格点平行四边形.
1. （1）把图1中的格点正方形分割成两部分，再通过图形变换拼成一个格点平行四边形，在图1中画出这个格点平行四边形.
2. （2）把图2中的格点正方形分割成三部分，再通过图形变换拼成一个格点平行四边形，在图2中画出这个格点平行四边形.
答案解析收藏纠错 + 选题

四、解答题

17. (2024八下·长兴期中) 如图，在 $\text{[math]}$ ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上，且AE=CF．
1. （1）求证：四边形EGFH是平行四边形；
2. （2）连结BD交AC于点O，若BD= 10，AE+CF=EF ，求EG的长．
答案解析收藏纠错 + 选题
18. 如图，在▱ABCD 中，延长 DA 到点 E，延长BC到点 F，使得 AE=CF，连结 EF，分别交AB，CD于点M，N，连结 DM，BN.求证：
1. （1） △AEM≌△CFN.
2. （2）四边形 BMDN 是平行四边形.
答案解析收藏纠错 + 选题

五、实践探究题

19. 问题：如图，在 $\text{[math]}$ ABCD中，AB=8，AD=5，∠DAB，∠ABC的平分线AE ，BF分别与直线CD交于点E，F，求EF的长．
答案：EF=2．
探究：
1. （1）把“问题”中的条件“AB= 8”去掉，其余条件不变．
  ①当点E与点F重合时，求AB的长；
  ②当点E与点C重合时，求EF的长．
2. （2）把“问题”中的条件“AB=8 ，AD=5”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求 $\text{[math]}$ 的值
答案解析收藏纠错 + 选题
20. (2023八下·巩义期末) 人教版初中数学教科书八年级下册第53页设置了如下一个“思考”栏目：
思考
如图2-3，矩形ABCD的对角线AC，BD相交于点O．我们观察 $\text{[math]}$ ，在 $\text{[math]}$ 中，BO是斜边AC上的中线，BO与AC有什么关系？

经过思考与探究，从而得到了直角三角形的一个性质：直角三角形斜边上的中线等于斜边的一半．
现在，我们一起来探究这条性质的证明过程：
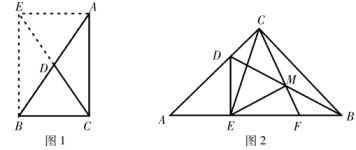
如图1：在 $\text{[math]}$ 中， $\text{[math]}$ ，CD是斜边AB上的中线．
求证： $\text{[math]}$ ．
证明：延长CD至点E，使 $\text{[math]}$ ，连接AE，BE．
……
1. （1）请你根据以上提示，结合图形，写出完整的证明过程．
2. （2）定理应用：
  如图2， $\text{[math]}$ 中， $\text{[math]}$ ，D为边AC上一点， $\text{[math]}$ 于点E，连接BD，M为BD的中点，CM的延长线交AB于点F，连接EC，EM．
  ①CM与EM的数量关系是．
  ②若BD是 $\text{[math]}$ 的平分线，且 $\text{[math]}$ ，则 $\text{[math]}$ °．
答案解析收藏纠错 + 选题
21. (2024七上·龙岗期末) 在数学实践活动课上，“卓越”小组准备研究如下问题：如图， $\text{[math]}$ 为直尺的一条边，四边形 $\text{[math]}$ 为一正方形纸板 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 均为直角 $\text{[math]}$
1. （1）【操作发现】
  如图 $\text{[math]}$ 小组成员小方把正方形的一条边 $\text{[math]}$ 与 $\text{[math]}$ 重合放置，刘老师在与同学们交流研讨时又做出了 $\text{[math]}$ 的平分线 $\text{[math]}$ ，交正方形的边于点 $\text{[math]}$ ．
  则此时 $\text{[math]}$ 的度数为； $\text{[math]}$ 与 $\text{[math]}$ 的度数之间的关系为．
2. （2）【问题探究】
  受小方同学的启发，小组成员小丽将正方形纸板按如图 $\text{[math]}$ 放置，若此时记 $\text{[math]}$ 的度数为 $\text{[math]}$ ，其他条件不变，请帮小丽同学探究： $\text{[math]}$ 与 $\text{[math]}$ 的度数之间的关系是否发生改变，并说明理由．
3. （3）【拓展延伸】
  组内其他同学也都继续探索，将正方形按如图 $\text{[math]}$ 放置，刘老师同样做出了 $\text{[math]}$ 的平分线 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的度数之间的关系．
答案解析收藏纠错 + 选题

六、综合题

22. (2024九下·娄底期中) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2023九上·滕州开学考) 已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．
1. （1）求证：△BCE≌△DCF；
2. （2）当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．
答案解析收藏纠错 + 选题
24. (2023九上·通城开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点C的直线 $\text{[math]}$ ， D为 $\text{[math]}$ 边上一点，过点D作 $\text{[math]}$ ，交直线 $\text{[math]}$ 于E，垂足为F，连接 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）当D在 $\text{[math]}$ 中点时，四边形 $\text{[math]}$ 是什么特殊四边形？请说明你的理由；
3. （3）若D为 $\text{[math]}$ 中点，则当 $\text{[math]}$ 的大小满足什么条件时，四边形 $\text{[math]}$ 是正方形？请说明你的理由．
答案解析收藏纠错 + 选题