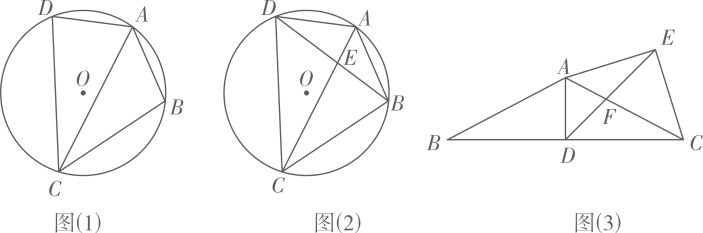
![]()
化简:
①甲同学:设制作A型盒个数为x,根据题意可得4x+3×=360;②乙同学:设制作B型盒用正方形纸板的张数为m,根据题意可得3×
+4(120-m)=360;③制作A型盒72个;④制作B型盒需正方形纸板共48张.

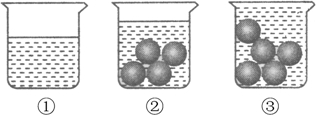
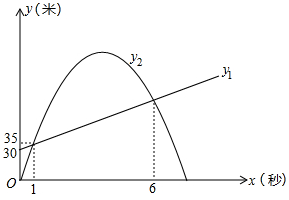
根据以上过程,推测这样一颗玻璃球的体积在( )
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 93 |
C | 15 | 5 | 65 |

用户 | 张大爷 | 刘奶奶 | 王阿姨 | 聪聪家 | 用户 |
输入( | 8 | 15 | 18 | 25 | 输入( |
输出(元) | 24 | a | 60 | b | 输出(元) |
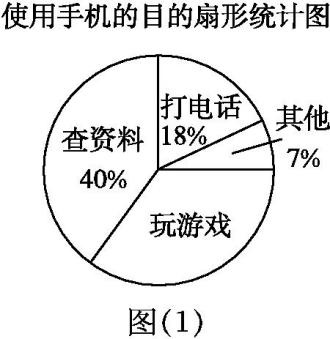
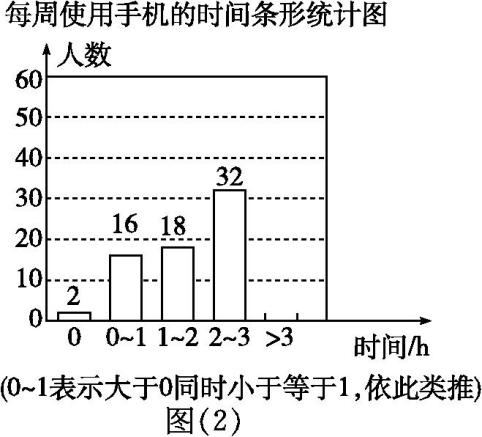
解答下列问题: