 B .
B . 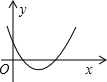 C .
C .  D .
D . 



| 素材1 | 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD= 12cm, 此时面汤最大深度EG= 6cm, |  |
| 素材2 | 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止. |  |
| 问题解决 | ||
| 任务1 | 确定碗体形状 | 在图2中建立合适的直角坐标系,求抛物线的函数表达式。 |
| 任务2 | 拟定设计方案1 | 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。 |
| 任务3 | 拟定设计方案2 | 如图3,当碗停止倾斜时,求此时碗中液面宽度CH。 |
综合与实践数学活动课上,张老师给出了一个问题:
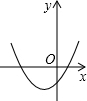
已知二次函数y=x2+2x-3,当-2≤x≤2时,y的取值范围为;
①小伟同学经过分析后,将原二次函数配方成y=a(x-h)2+k
形式,确定抛物线对称轴为直线x=h , 通过-2、h和2的大小
关系,分别确定了最大值和最小值,进而求出y的取值范围;
②小军同学画出如图的函数图象,通过观察图象确定了y的取值范围;请你根据上述两名同学的分析写出y的取值范围是;
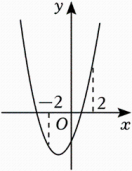
张老师发现两名同学分别从“数”和“形”的角度分析、解决问题,为了让同学们更好感悟“数形结合”思想,张老师将前面问题变式为下面问题,请你解答:已知二次函数y=-x2+2x-3,当-2≤x≤2时,求y的取值范围;
已知二次函数y=-x2+6x-5,当a≤x≤a+3时,二次函数的最大值为y1 , 最小值为y2 , 若y1-y2=3,求a的值.
素材1 | 某学校一块劳动实践基地大棚的横截面如图所示,上部分的顶棚是抛物线形状,下部分是由两根立柱 |
| |
素材2 | 为提高灌溉效率,学校在 |
| |
问题解决 | |||
任务1 | 确定顶棚的形状 | 以顶棚最高点为坐标原点建立平面直角坐标系,求出顶棚部分抛物线的表达式. | |
任务2 | 探索喷水的高度 | 问 | |
任务3 | 调整喷头的高度 | 如何调整喷水口的高度(形状不变),使水流喷灌时恰好落在边缘 | |

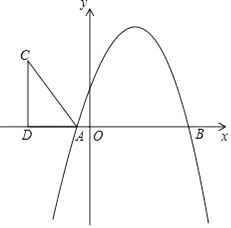
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;