2024年北师大版数学七（下）重难点培优训练2 平方差公式和...

更新时间：2024-04-13 浏览次数：37 类型：复习试卷

一、选择题

1. (2024八上·黔西南期末) 若 $\text{[math]}$ 是完全平方式，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . 12 C . $\text{[math]}$ 或11 D . $\text{[math]}$ 或12

答案解析收藏纠错 + 选题
2. (2023七下·石家庄期中) 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如4=2²-0² ， 12=4²-2² ， 20=6²-4² ，因此4，12，20都是“神秘数”，则下面哪个数是“神秘数”(　　)

A . 56 B . 66 C . 76 D . 86

答案解析收藏纠错 + 选题
3. (2024七下·新宁期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 25 B . 1 C . 21 D . 29

答案解析收藏纠错 + 选题
4. (2023七下·长春月考) 如图分割的正方形，拼接成长方形的方案中，可以验证（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 下列各式中，不能用平方差公式计算的是（）

A . (x-2y)(2y+x) B . (x-2y)(-x-2y) C . (x+2y)(-x-2y) D . (2y-x)(-x-2y)

答案解析收藏纠错 + 选题
6. (2023七下·江阴期中) 一个正整数若能表示为两个正整数的平方差，则称这个正整数为“创新数”，例如27＝6²-3² ， 63＝8²-1² ，故27，63都是“创新数”，下列各数中，不是“创新数”的是（）

A . 31 B . 41 C . 16 D . 54

答案解析收藏纠错 + 选题
7. (2023七下·沭阳期中) 计算 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 下列运算中，错误的运算有（）.
①(2x+y)²=4x²+y²
②(a-3b)²=a²-9b²
③(-x-y)²=x²-2xy+y²
④(x- $\text{[math]}$ )²=x²-2x+ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2023七下·南山期中) 我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉 $\text{[math]}$ 约 $\text{[math]}$ 世纪 $\text{[math]}$ 所著的 $\text{[math]}$ 详解九章算术 $\text{[math]}$ 一书中，用如图的三角形解释二项和 $\text{[math]}$ 的展开式的各项系数，此三角形称为“杨辉三角”，根据“杨辉三角”计算 $\text{[math]}$ 的展开式中第三项的系数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023七下·渠县期末) 下列运算：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题

二、填空题

11. (2023八上·剑河月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023七下·云岩期中) 如图，长为a，宽为b的长方形的周长为16，面积为12，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2023七下·石阡期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2023七下·石家庄期中) 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为 $\text{[math]}$ ；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为 $\text{[math]}$ ．当 $\text{[math]}$ + $\text{[math]}$ ＝40时，则图3中阴影部分的面积 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
15. (2023七下·顺义期中) 观察下列各式的规律： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 请将发现的规律用含 $\text{[math]}$ 的式子表示为．

答案解析收藏纠错 + 选题
16. (2024七下·沈阳月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的个位数字是．

答案解析收藏纠错 + 选题

三、计算题

17. (2023七下·金溪期中) 运用乘法公式计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023七下·即墨期中) 计算：
1. （1） $\text{[math]}$ ．
2. （2） $\text{[math]}$ ．
3. （3） $\text{[math]}$ ．
4. （4） $\text{[math]}$ ．（用简便方法计算）
答案解析收藏纠错 + 选题

四、综合题

19. (2023七下·凤翔期中) 聪聪和同学们用2张 $\text{[math]}$ 型卡片、2张 $\text{[math]}$ 型卡片和1张 $\text{[math]}$ 型卡片拼成了如图所示的长方形．其中 $\text{[math]}$ 型卡片是边长为 $\text{[math]}$ 的正方形； $\text{[math]}$ 型卡片是长方形； $\text{[math]}$ 型卡片是边长为 $\text{[math]}$ 的正方形．
1. （1）请用含a、b的代数式分别表示出 $\text{[math]}$ 型卡片的长和宽；
2. （2）如果 $\text{[math]}$ ， $\text{[math]}$ ，请求出他们用5张卡片拼出的这个长方形的面积．
答案解析收藏纠错 + 选题
20. (2022七下·义乌期中) 你会求（a－1）（a²⁰¹²＋a²⁰¹¹＋a²⁰¹⁰＋‥‥a²＋a＋1）的值吗？这个问题看上去很复杂，我们可以先考虑简单的情况，通过计算，探索规律：
（a－1）（a＋1）＝a²－1
（a－1）（a²＋a＋1）＝a³－1；
（a－1）（a³＋a²＋a＋1）＝a⁴－1；
1. （1）由上面的规律我们可以大胆猜想，得到（a－1）（a²⁰¹²＋a²⁰¹¹＋a²⁰¹⁰＋……a²＋a＋1）＝.
2. （2）利用上面的结论，求2²⁰¹³＋2²⁰¹²＋2²⁰¹¹＋……2²＋2＋1的值是.
3. （3）求5²⁰¹³＋5²⁰¹²＋5²⁰¹¹＋……5²＋5＋1的值.
答案解析收藏纠错 + 选题
21. (2023七下·深圳期中) 在数学中，有许多关系都是在不经意间被发现的，请认真观察图形，解答下列问题：
1. （1）如图1，用两种不同的方法表示阴影图形的面积，得到一个等量关系：．
2. （2）如图1中， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
3. （3）如图2，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，以 $\text{[math]}$ ， $\text{[math]}$ 为边向两边作正方形， $\text{[math]}$ ，两正方形的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求图中阴影部分面积．
答案解析收藏纠错 + 选题
22. (2023七下·宝安期中) 【项目学习】配方法是数学中重要的一种思想方法，它是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
例如，把二次三项式 $\text{[math]}$ 进行配方

解： $\text{[math]}$

我们定义：一个整数能表示成 $\text{[math]}$ （a，b是整数）的形式，则称这个数为“完美数”例如，5是“完美数”，理由：因为 $\text{[math]}$ ，再如， $\text{[math]}$ ，（x，y是整数）所以M也是“完美数”
1. （1）【问题解决】
  下列各数中，“完美数”有．（填序号）
  ①10 ②45 ③28 ④29
2. （2）若二次三项式 $\text{[math]}$ （ $\text{[math]}$ 是整数）是“完美数”，可配方成 $\text{[math]}$ （m， $\text{[math]}$ 为常数），则 $\text{[math]}$ 的值为；
3. （3）【问题探究】
  已知 $\text{[math]}$ （x，y是整数，k是常数），要使S为“完美数”，试求出符合条件的k的值．
4. （4）【问题拓展】
  已知实数x，y满足 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
23. (2023七下·石阡期中) 如图1，边长为 $\text{[math]}$ 的正方形中有一个边长为 $\text{[math]}$ 的小正方形，图2是由图1中阴影部分拼成的一个长方形，设图1中阴影部分面积为 $\text{[math]}$ ，图2中阴影部分面积为 $\text{[math]}$ ．
1. （1）请直接用含 $\text{[math]}$ 和 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ， $\text{[math]}$ ；写出利用图形的面积关系所得到的公式：（用式子表示）．
2. （2）依据这个公式，康康展示了“计算： $\text{[math]}$ ”的解题过程．
  解：原式 $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$ ．
  请仿照康康的解题过程计算： $\text{[math]}$ ．
3. （3）对数学知识要会举一反三，请用（1）中的公式证明：任意两个相邻奇数的平方差必是 $\text{[math]}$ 的倍数．
答案解析收藏纠错 + 选题
24. (2024·南山模拟) 对于一个图形，通过两种不同的方法计算它们的面积，可以得到一个数学等式．例如图1可以得到 $\text{[math]}$ ，请解答下列问题：
1. （1）如图2，需要张边长为a的正方形，张边长为b的正方形，张边长为a、b的长方形．
2. （2）类似图1的数学等式，写出图2表示的数学等式：．
3. （3）用多项式乘多项式的法则验证（2）中得到的等式．
答案解析收藏纠错 + 选题
25. (2023七下·龙岗期中) 如图(a)所示，边长为a的大正方形中有一个边长为b的小正方形，把图(a)中的阴影部分拼成一个如图(b)所示的长方形．
1. （1）通过观察比较图(b)与图(a)中的阴影部分面积，可以得到乘法公式(用含a，b的等式表示)
2. （2） (应用)请应用这个公式完成下列各题：
  ①若a+2b=3，2b-a=2，则a²-4b²的值为
  ②若4m²=12+n，2m+n=4，则2m-n的值为
3. （3） (拓展)计算：100² -992+98²-97²+……+4²-3²+2²-1² ．
答案解析收藏纠错 + 选题
26. (2022七下·咸阳期中) 阅读材料：若满足（8-x）（x-6）=-3，求（8-x）²+（x-6）²的值．
解：设8-x=a，x-6=b，则（8-x）（x-6）=ab=-3，a+b=8-x+x-6=2
所以（8-x）²+（x-6）²=a²+b²=（a+b）²-2ab=2²-2×（-3）=10
请仿照上例解决下面的问题：
1. （1）问题发现：若x满足（3-x）（x-2）=-10，求（3-x）²+（x-2）²的值；
2. （2）若（6-x）²+（x-4）²=8求（6-x）（x-4）的值；
3. （3）类比探究：若x满足（2022-x）²+（2021-x）²=2020；求（2022-x）（2021-x）的值；
答案解析收藏纠错 + 选题
27. (2021七下·娄底期中) 阅读材料并回答问题：
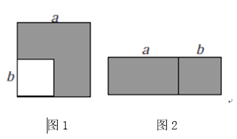
我们知道，完全平方公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，如（2a+b）（a+b）＝2a²+3ab+b²就可以用图①或图②中图形的面积表示.
1. （1）请写出图③所表示的代数恒等式；
2. （2）试画一个几何图形，使它的面积可用（a+b）（a+3b）＝a²+4ab+3b²表示；
3. （3）请依照上述方法另写一个含有a，b的代数恒等式，并画出它对应的几何图形.
答案解析收藏纠错 + 选题
28. (2022七下·连云港期中)
1. （1）【知识情境】通常情况下，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式.
  如图1，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b） .把余下的部分剪拼成一个长方形（如图2）.通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是；
2. （2）【拓展探究】类似地，用两种不同的方法计算同一个几何体的体积，也可以得到一个恒等式.
  如图3是边长为 $\text{[math]}$ 的正方体，被如图所示的分割线分成8块.
  
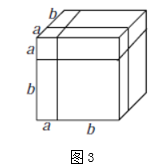
  用不同的方法计算这个正方体的体积，就可以得到一个恒等式，这个恒等式可以为：
  
  ；
3. （3）已知 $\text{[math]}$ ， $\text{[math]}$ ，利用上面的恒等式求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
29. (2022七下·定远期中) 【阅读材料】
我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数关系，而运用代数思想也能巧妙地解决一些图形问题．
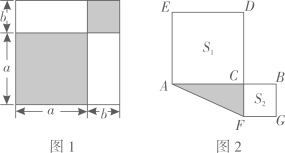
在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y，宽为x的长方形，并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形．
1. （1）【理解应用】
  观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式；
2. （2）【拓展升华】
  利用（1）中的等式解决下列问题
  ①已知 $\text{[math]}$ ， $\text{[math]}$ ，求ab的值；
  ②已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题