B .
B .  C .
C .  D .
D . 
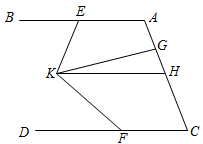
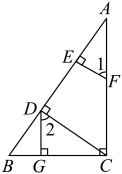
证明:∵ ,
(已知)
∴ ,
(垂直定义)
∴
∴( )
∴ ▲ ( )
∵(已知)
∴ ▲ (等量代换)
∴( )
∴ ▲ ( )
∵(已知)
∴(垂直定义)
∴ ▲
(等量代换)
∴(垂直定义)
因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:、
等,而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料一:∵ , 即
,
∴ .
∴的整数部分为1.
∴的小数部分为
.
材料二:我们还可以用以下方法求一个无理数的近似值.
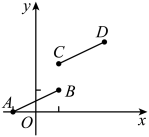
我们知道面积是2的正方形的边长是 , 易知
, 因此可设
, 可画出如图示意图.由图中面积计算,
, 另一方面由题意知
, 所以
.
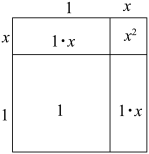
略去 , 得方程
, 解得
, 即
.
解决问题:

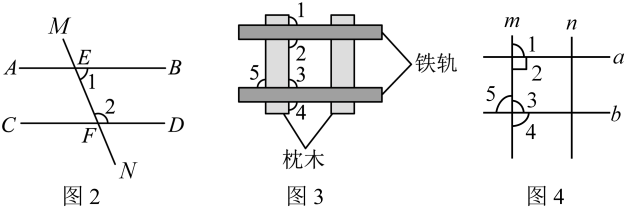
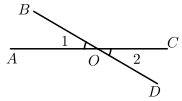
已知:如图2,∠1和∠2是直线被直线
截出的同旁内角,且
与
互补,求证:
. (推理过程请注明理由)
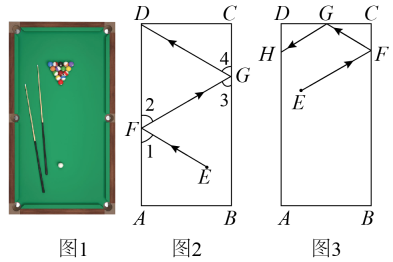
台球中的数学
如图1是台球桌面实物图,图2是抽象出的数学图形,已知长方形桌面中,
, 一个球在桌面上的点
处滚向桌边
, 碰到
上的点
后反弹,再碰到
边上的点
后,再次反弹进入底袋点
. 在球碰到桌边反弹的过程中,击出线与桌边的夹角
等于反弹线与桌边的夹角
, 同理
.