一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
-
A . -1
B . -4
C . 4
D . 1
-
-
3.
若

, 则
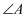
的补角为 ( )
-
-
5.
(2024·白银)
如图,在矩形
ABCD中,对角线
AC ,
BD相交于点

, 则
AC的长为 ( )

A . 6
B . 5
C . 4
D . 3
-
-
7.
(2024·白银)
如图1“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图2给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为

尺,长桌的长为

尺,则

与

的关系可以表示为 ( )

-
8.
(2024·武威)
近年来,我国重视农村电子商务的发展.下面的统计图反映了2016-2023年中国农村网络零售额情况.根据统计图提供的信息,下列结论错误的是 ( )

A . 2023年中国农村网络零售额最高
B . 2016年中国农村网络零售额最低
C . 2016-2023年,中国农村网络零售额持续增加
D . 从2020年开始,中国农村网络零售额突破20000亿元
-
9.
(2024·白银)
敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10步到60步的矩形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )

A . 一亩八十步
B . 一亩二十步
C . 半亩七十八步
D . 半亩八十四步
-
10.
(2024九上·龙岗期中)
如图1,动点
P从菱形
ABCD的点
A出发,沿边
AB→
BC匀速运动,运动到点
C时停止.设点

的运动路程为
x ,
PO的长为
y ,
y与

的函数图象如图2所示,当点

运动到
BC中点时,
PO的长为 ( )

A . 2
B . 3
C .  D .
D . 
二、填空题:本大题共6小题,每小题4分,共24分.
-
-
12.
(2024·武威)
已知一次函数

, 当自变量

时,函数

的值可以是
(写出一个合理的值即可).
-
-
14.
(2024·白银)
围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点
的位置,则所得的对弈图是轴对称图形.(填写

中的一处即可,

位于棋盘的格点上)

-
15.
(2024·武威)
如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度
y(单位:m)与距离停车棚支柱
AO的水平距离
x(单位:m)近似满足函数关系

的图象,点

在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长

, 高

的矩形,则可判定货车
完全停到车棚内(填“能”或“不能”).

-
16.
(2024·白银)
甘肃临夏砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产.如图1是一块扇面形的临夏砖雕作品,它的部分设计图如图2,其中扇形
OBC和扇形
OAD有相同的圆心

, 且圆心角

, 若

, 则阴影部分的面积是

.(结果用π表示)

三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过珵或演算步骤.
-
-
-
-
20.
(2024·白银)
马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知

和圆上一点
M.作法如下:
①以点 为圆心,OM长为半径,作弧交
为圆心,OM长为半径,作弧交 于A , B两点;
于A , B两点;
②延长MO交 于点
于点 ;
;
即点 将
将 的圆周三等分.
的圆周三等分.

-
(1)
请你依据以上步骤,用不带刻度的直尺和圆规在图2中将

的圆周三等分(保留作图痕迹,不写作法);
-
(2)
根据(1)画出的图形,连接

若

的半径为

, 则

的周长为
cm.
-
21.
(2024·白银)
在一只不透明的布袋中,装有质地、大小均相同的四个小球,小球上分别标有数字1,2,3,4.甲乙两人玩摸球游戏,规则为:两人同时从袋中随机各摸出1个小球,若两球上的数字之和为奇数,则甲胜;若两球上的数字之和为偶数,则乙胜.
-
(1)
请用画树状图或列表的方法,求甲获胜的概率.
-
(2)
这个游戏规则对甲乙双方公平吗?请说明理由.
-
22.
(2024·武威)
习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速,某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒
AH垂直于地面,测角仪

在
AH两侧,

, 点

与点

相距

(点

在同一条直线上),在
D处测得筒尖顶点

的仰角为

, 在

处测得筒尖顶点

的仰角为

.求风电塔筒
AH的高度.(参考数据:

.)

四、解答题:本大题共5小题,共50分,解答时,应写出必要的文字说明、证明过程或演算步骤.
-
23.
(2024·白银)
在阳光中学运动会跳高比赛中,每位选手要进行五轮比赛,张老师对参加比赛的甲、乙、丙三位选手的得分(单位:分,满分10分)进行了数据的收集、整理和分析,信息如下:
信息一:甲、丙两位选手的得分折线图:

信息二:选手乙五轮比赛部分成绩:其中三个得分分别是9.0,8.9,8.3;
信息三:甲、乙、丙三位选手五轮比赛得分的平均数、中位数数据如下:
选手 统计量 | 甲 | 乙 | 丙 |
平均数 | m | 9.1 | 8.9 |
中位数 | 9.2 | 9.0 | n |
根据以上信息,回答下列问题:
-
-
(2)
从甲、丙两位选手的得分折线图中可知,选手发挥的稳定性更好(填“甲”或“丙”);
-
(3)
该校现准备推荐一位选手参加市级比赛,你认为应该推荐哪位选手,请说明理由.
-
24.
(2024·武威)
如图,在平面直角坐标系中,将函数

的图象向上平移3个单位长度,得到一次函数

的图象,与反比例函数

的图象交于点

.过点

作

轴的平行线分别交

与

的图象于
C ,
D两点.

-
(1)
求一次函数

和反比例函数

的表达式;
-
(2)
连接
AD , 求

的面积.
-
-
(1)
求证:
BE是

的切线;
-
-
-
(1)
【模型建立】
如图1,已知 和
和 .用等式写出线段
.用等式写出线段 的数量关系,并说明理由.
的数量关系,并说明理由.
-
(2)
【模型应用】
如图2,在正方形ABCD中,点E , F分别在对角线BD和边CD上, ,
,  .用等式写出线段
.用等式写出线段 的数量关系,并说明理由.
的数量关系,并说明理由.
-
-
-
(1)
求拋物线

的表达式;
-
(2)
过点
C作

, 垂足为

, 交抛物线于点

.求线段
CE的长.
-
(3)
点
D为线段
OA上一动点(
O点除外),在
OC右侧作平行四边形
OCFD.
①如图2,当点F落在抛物线上时,求点 的坐标;
的坐标;
②如图3,连接 , 求
, 求 的最小值.
的最小值.

为圆心,OM长为半径,作弧交
于A , B两点;
于点
;
将
的圆周三等分.

