浙教版数学八年级暑假知识训练：正多边形

更新时间：2024-06-30 浏览次数：21 类型：复习试卷

一、选择题（每题3分，共30分）

1. (2024九下·西城模拟) 正十二边形的一个外角的度数为（）

A . 30° B . 36° C . 144° D . 150°

答案解析收藏纠错 + 选题
2. (2023九上·金华月考) 已知正多边形的一个外角等于45°，那么这个正多边形的边数为（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
3. (2024九上·昭通期末) 一个圆的内接正多边形中，一条边所对的圆心角为72°，则该正多边形的边数是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
4. (2024九上·五华期末) 一个半径为2cm的圆的内接正六边形的面积是（　　）

A . 24cm² B . 6 $\text{[math]}$ cm² C . 12 $\text{[math]}$ cm² D . 8 $\text{[math]}$ cm²

答案解析收藏纠错 + 选题
5. (2023九上·定海月考) 正十边形的每个内角都是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·永康期中) 边长为6的正三角形的外接圆的半径为（）

A . 2 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ π D . 2 $\text{[math]}$ π

答案解析收藏纠错 + 选题
7. 如图，正六边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，正六边形的周长是12，则 $\text{[math]}$ 的半径是（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·温州期中) 利用圆的等分，在半径为 $\text{[math]}$ 的圆中作出六芒星图案，则图中阴影部分的面积为（）

A . 6 B . $\text{[math]}$ C . 12 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·杭州期中) 如图，正六边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，若 $\text{[math]}$ 的周长是 $\text{[math]}$ ，则正六边形的边长是（）

A . $\text{[math]}$ B . 3 C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·滨江期中) 作⊙O的内接正六边形ABCDEF ，甲、乙两人的作法分别是：
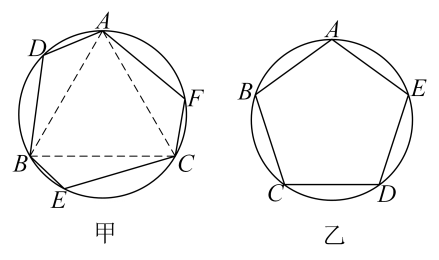
甲：第一步：在⊙O上任取一点A ，从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B ， C ， D ， E ， F ．第二步：依次连接这六个点．
乙：第一步：任作一直径AD ．第二步：分别作OA ， OD的中垂线与⊙O相交，交点从点A开始，依次为点B ， C ， E ， F ．第三步：依次连接这六个点．
对于甲、乙两人的作法，可判断（）

A . 甲正确，乙错误 B . 甲、乙均错误 C . 甲错误，乙正确 D . 甲、乙均正确

答案解析收藏纠错 + 选题

二、填空题（每题4分，共24分）

11. (2024八下·中卫期末) 已知正n边形的每一个内角都等于144°，则n的值为.

答案解析收藏纠错 + 选题
12.
1. （1）已知正多边形的一个内角为135°，则该正多边形是正边形．
2. （2）已知一个正多边形的每个外角都等于36°，那么它是正边形．
答案解析收藏纠错 + 选题
13. (2024九下·吴川期中) 若一个正多边形的每个内角为150°，则这个正多边形的边数是．

答案解析收藏纠错 + 选题
14. (2023九上·洞头期中) 如图，正五边形ABCDE内接于⊙O，则∠ABD＝．

答案解析收藏纠错 + 选题
15. (2023九上·温州期末) 如图，在正六边形ABCDEF中，以点A为原点建立直角坐标系，边AB落在x轴上．若点B的坐标为(2，0)，则点C的坐标是．

答案解析收藏纠错 + 选题
16. (2024九上·宁波期末) 刘徽是我国魏晋时期卓越的数学家，他首次提出“割圆术”，利用圆内接正多边形逐步逼近圆来近似计算圆周率，方法如图：作正六边形ABCDEF内接于 $\text{[math]}$ ，取 $\text{[math]}$ 的中点G， $\text{[math]}$ 与 $\text{[math]}$ 交于点H；连接 $\text{[math]}$ 、 $\text{[math]}$ ；依次对剩余五段弧取中点可得一个圆内接正十二边形，记正十二边形的面积为 $\text{[math]}$ ，正六边形的面积为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题（共8题，共66分）

17. (2019九上·桥东月考)
如图，以正六边形ABCDEF的边AB为边，在形内作正方形ABMN，连接MC．求∠BCM的大小．

答案解析收藏纠错 + 选题
18. (2023九上·无为月考) 如图，正八边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， M是弧DE上的一点，连接AM ， BM ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
19. 已知：如图，在圆内接正五边形ABCDE中，对角线AC，BD交于点P．
1. （1）求∠APD的度数．
2. （2）求证：四边形EAPD是菱形．
答案解析收藏纠错 + 选题
20. 已知：如图，正六边形ABCDEF的边长为6cm，延长FE，CD，相交于点G．
1. （1）求证：△FCG是正三角形．
2. （2）求正三角形FCG的高线长．
答案解析收藏纠错 + 选题
21. 如图，正方形ABCD的外接圆为⊙O，点P在劣弧 CD上（不与C点重合）．
1. （1）求∠BPC的度数；
2. （2）若⊙O的半径为8，求正方形ABCD的边长．
答案解析收藏纠错 + 选题
22. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切（我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形）．
1. （1）设T₁ ， T₂的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；
2. （2）求正六边形T₁ ， T₂的面积比S₁：S₂的值．
答案解析收藏纠错 + 选题
23. (2024九上·缙云期末) 如图 $\text{[math]}$ ，小吴同学在陶艺课中为八角花盆制作“圆形托盘”，已知八角花盆底部截面是一个正八边形（如图 $\text{[math]}$ ），请根据下列信息解决问题．
1. （1）求八角花盆底部截面正八边形一个内角的度数；
2. （2）若八角花盆底部截面正八边形的边长是 $\text{[math]}$ ，小吴同学制作的圆形托盘半径是 $\text{[math]}$ ，问：这个托盘是否适用于此八角花盆？（图 $\text{[math]}$ 中边长的数据为近似值，供选用）
答案解析收藏纠错 + 选题
24. 某数学学习小组的成员在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行了如下探讨：
甲同学：我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学：但是边数为3时，它是正三角形，而且我猜想，边数为5时，它应该是正五边形……
丙同学：我发现边数为6时，它也不一定是正六边形.如图甲所示， $\text{[math]}$ 是正三角形， $\text{[math]}$ 均相等，很显然由此构造的六边形ADBECF并不是正六边形.
1. （1）如图乙所示，若圆内接五边形ABCDE的各内角均相等，则∠ABC= .请简要说明圆内接五边形ABCDE为正五边形的理由.
2. （2）请证明丙同学构造的六边形各内角相等.
3. （3）根据以上的探索过程，就“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3，n为整数)”的关系，请提出你的猜想.(不需证明)
答案解析收藏纠错 + 选题