试验种子数n(粒) | 50 | 200 | 500 | 1000 | 3000 |
发芽频数m | 45 | 188 | 476 | 951 | 2850 |
发芽频率 | 0.9 | 0.94 | 0.952 | 0.951 | 0.95 |

| 种子数量 | 200 | 500 | 800 | 1500 | 3000 | |
| A | 出芽率 | 0.98 | 0.94 | 0.96 | 0.98 | 0.97 |
| B | 出芽率 | 0.98 | 0.95 | 0.94 | 0.97 | 0.96 |
下面在三个推断:
①当实验种子数员为200时,两种种子的出芽率均为0.98,所以两种新五米种子出芽的概率一样;
②随着实验种子数量的增加,种子出芽率在0.96附近摆动,显示出一定的稳定性,可以估计
种子出芽的概率是0.96:
③在同样的地质环境下播种,种子的出芽率可能会离于
种子.
其中合理的是( )

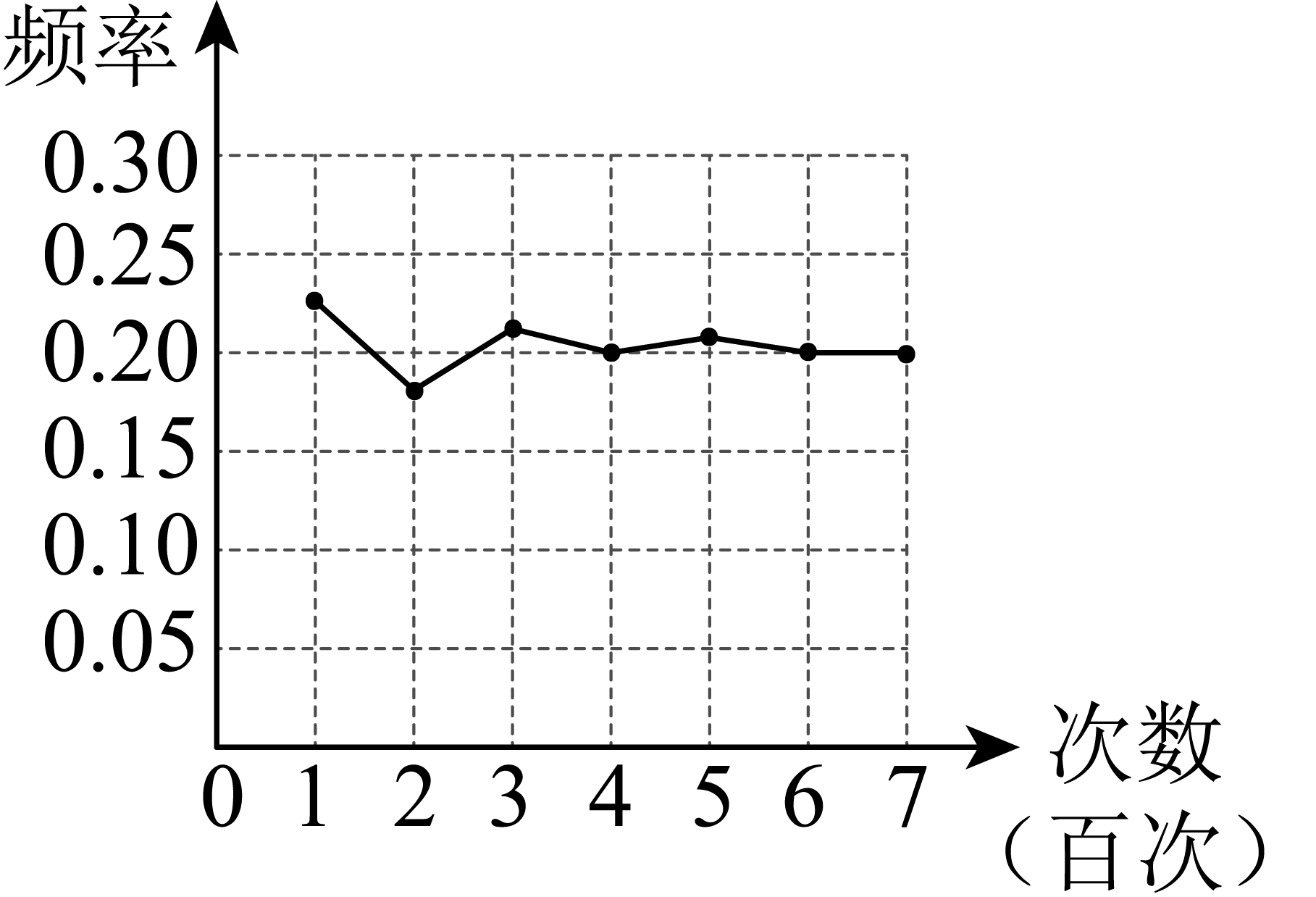

下面有四个推断:
①当投掷次数是600时,计算机记录“钉尖向上”的次数是400,所以“钉尖向上”的概率是0.667;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620;
④若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的情况一定高于500次.
其中合理的是( )


试验次数 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 | 5000 |
相交频数 | 495 | 623 | 799 | 954 | 1123 | 1269 | 1434 | 1590 |
相交频率 |
可以估计出针与直线相交的概率为(精确到),由此估计
的近似值为(精确到
).
种子数量 | ||||||
发芽率 | ||||||
发芽率 | ||||||
下面有两个推断:当实验种子数量为
时,两种种子的发芽率均为
, 所以
,
两种新水稻种子发芽的概率一样;
随着实验种子数量的增加,
种子发芽率在
附近摆动,显示出一定的稳定性,可以估计
种子发芽的概率是
. 其中合理的是.
空气质量等级 | 空气质量指数(AQI) | 频数 |
优 | AQI≤50 | m |
良 | 50<AQI<1100 | 15 |
中 | 100<AQI≤150 | 9 |
差 | AQI>150 | n |

摸球的次数 | ||||||
摸到白球的次数 | ||||||
摸到白球的频率 |
实验总次数 | 10 | 50 | 100 | 500 | 1000 | 2000 | 5000 | 10000 | 20000 | 50000 |
“和为8”的次数 | 2 | 25 | 43 | 191 | 334 | 619 | 1608 | 3397 | 6622 | 16499 |
“和为8”的频率(结果保留两位小数) | 0.20 | 0.50 | 0.43 | 0.38 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
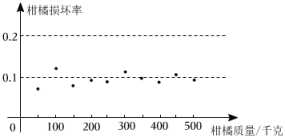
| 特级柑橘的售价(元/千克) | 14 | 15 | 16 | 17 | 18 |
| 特级柑橘的日销售量(千克) | 1000 | 850 | 900 | 850 | 800 |