【提升版】北师大版数学九年级上册 4.2平行线分线段成比例 ...

更新时间：2024-10-18 浏览次数：4 类型：同步测试

一、选择题

1. (2024九上·金沙期末) 如图，直线 $\text{[math]}$ ，直线a ， b相交于点 $\text{[math]}$ ，且与 $\text{[math]}$ 分别相交于点B ， C和点D ， E ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·铜仁期末) 如图是某景区大门部分建筑，已知 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 时，则 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·深圳月考) 如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
4. (2024九上·嘉兴期末) 如图，点 $\text{[math]}$ 是等边三角形 $\text{[math]}$ 的重心， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，当 $\text{[math]}$ 时，则 $\text{[math]}$ 的长为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
5. (2023九上·衡阳期末) 如图，若 $\text{[math]}$ ，则下列各式错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·威远期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ，则下列比例式不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·溆浦期中) 如图，已知 $\text{[math]}$ ，它们依次交直线 $\text{[math]}$ 于点A、B、C和点D、E、F ，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的长等于（）

A . 2 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·平顶山期末) 如图，矩形 $\text{[math]}$ 的四个顶点分别在直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上，若直线 $\text{[math]}$ 且相邻两直线间距离相等．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 之间的距离为（）．

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·丰顺期末) 如图，在Rt△ABC中，∠ACB＝90°，AB=10，BC＝6．点F是AB中点，连接CF，把线段CF沿射线BC方向平移到DE，点D在AC上．则线段CF在平移过程中扫过区域形成的四边形CFDE的面积为．

答案解析收藏纠错 + 选题
10. (2024九下·榆树开学考) 如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在横格线上 $\text{[math]}$ 若线段 $\text{[math]}$ ，则线段 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九上·仁寿期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024九上·永修模拟) 如图，已知菱形 $\text{[math]}$ 的边长为4， $\text{[math]}$ ， E为 $\text{[math]}$ 的中点，F为 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 相交于点G，则 $\text{[math]}$ 的长等于．

答案解析收藏纠错 + 选题
13. (2024九上·泸县模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线，点E在 $\text{[math]}$ 上， $\text{[math]}$ 交 $\text{[math]}$ 于点F．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

14. (2024九下·榆树月考) 如图， $\text{[math]}$ ，直线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，且分别与直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 和点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度是？

答案解析收藏纠错 + 选题
15. (2024九上·钟山期末) 如图，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形ABCD时菱形；
2. （2）延长BC至点M ，连接OM交CD于点N ，若 $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. (2019九上·太原期中) 阅读下列材料，完成相应的任务：
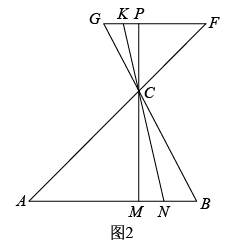
我们知道，利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢？如图，已知线段MN，用尺规在MN上求作点P，使 $\text{[math]}$ .

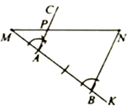
小颖的作法是：

①作射线MK（点K不在直线MN上）；

②在射线MK上依次截取线段MA，AB，使 $\text{[math]}$ ，连接BN；

③作射线 $\text{[math]}$ ，交MN于点P点P即为所求作的点.

小颖作法的理由如下：

∵ $\text{[math]}$ （作法），∴ $\text{[math]}$

∵ $\text{[math]}$ （已知）， $\text{[math]}$ （等量代换）

∵ $\text{[math]}$ （线段和差定义），∴ $\text{[math]}$ （等量代换，等式性质）
1. （1）数学思考：
  小颖作法理由中所缺的依据是：.
2. （2）拓展应用：
  如图，已知线段a，b，c，求作线段d，使 $\text{[math]}$ a. B. C.
答案解析收藏纠错 + 选题
17. (2022九上·新昌月考) 定义：如图1，点 $\text{[math]}$ 、 $\text{[math]}$ 把线段 $\text{[math]}$ 分割成三条线段 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ ，若 $\text{[math]}$ ，则称 $\text{[math]}$ 是线段 $\text{[math]}$ 的比例中段， $\text{[math]}$ 、 $\text{[math]}$ 是线段 $\text{[math]}$ 的中段分点.
1. （1）已知点 $\text{[math]}$ 、 $\text{[math]}$ 是线段 $\text{[math]}$ 的中段分点.
  ①若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ▲ ；
  ②在图1中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
2. （2）如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 是线段 $\text{[math]}$ 的比例中段， $\text{[math]}$ 、 $\text{[math]}$ 分别是线段 $\text{[math]}$ 、 $\text{[math]}$ 延长线上的点，且 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 的延长线分别交线段 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ .探究 $\text{[math]}$ 是否为线段 $\text{[math]}$ 的比例中段，如果是，请给出证明，如果不是，请说明理由..
答案解析收藏纠错 + 选题