【培优版】北师大版数学九年级上册4.4探索三角形相似的条件 ...

更新时间：2024-09-28 浏览次数：6 类型：同步测试

一、选择题

1. (2023九上·余杭期中) 如图，将矩形ABCD沿着GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，点E，O，F 在另一条直线上. 以下结论正确的是（）

A . △COF∽△CEG B . OC=3OF C . AB：AD=4：3 D . GE= $\text{[math]}$ DF

答案解析收藏纠错 + 选题
2. (2020九上·子洲期中) 如图，四边形 $\text{[math]}$ 是边长为2的正方形点P为线段 $\text{[math]}$ 上的动点，E为 $\text{[math]}$ 的中点，射线 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点Q，过点E作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 于点H.交 $\text{[math]}$ 的延长线于点F，则以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③当点F与点C重合时 $\text{[math]}$ ；④当 $\text{[math]}$ 时， $\text{[math]}$ .成立的是（）

A . ①②③ B . ①③④ C . ②③④ D . ②④

答案解析收藏纠错 + 选题
3. (2018九上·温州期中) 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法．如图所示，以线段AB为边作正方形ABCD，取AD的中点E，连结BE，延长DA至F，使得EF=BE，以AF为边作正方形AFGH，则点H即是线段AB的黄金分割点．若记正方形AFGH的面积为S₁ ，矩形BCIH的面积为S₂ ，则S₁ 与S₂的大小关系是（）

A . B . C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
4. (2019九上·长兴期末) 如图，点A，B，C，D的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，以点C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（）

A . (6，5) B . (6，0) C . (6，4) D . (4，2)

答案解析收藏纠错 + 选题
5. (2023九上·石家庄期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，用直尺和圆规在AB上确定点D ，使 $\text{[math]}$ ，根据作图痕迹判断，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022九上·凤阳月考) 如图，在 $\text{[math]}$ 中，点D，E分别是 $\text{[math]}$ ， $\text{[math]}$ 上的点， $\text{[math]}$ 与 $\text{[math]}$ 交于点F，下列条件中不能使 $\text{[math]}$ 和 $\text{[math]}$ 相似的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·石家庄期中)
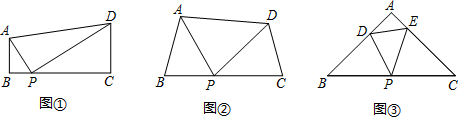
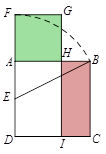
如图，在钝角三角形ABC中，AB=6cm，AC=12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（　　）

A . 4或4.8 B . 3或4.8 C . 2或4 D . 1或6

答案解析收藏纠错 + 选题
8. (2023九上·永州月考) 如图正方形 $\text{[math]}$ ，点 $\text{[math]}$ 分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，把 $\text{[math]}$ 绕点 $\text{[math]}$ 沿逆时针方向旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，并在 $\text{[math]}$ 上截取 $\text{[math]}$ ，连接 $\text{[math]}$ ，有如下结论：① $\text{[math]}$ ；② $\text{[math]}$ 始终平分 $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ 垂直平分 $\text{[math]}$ ，上述结论中，所有正确的个数是（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题

二、填空题

9. (2023九上·武侯期中) 在平面直角坐标系xOy中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A₁ ，作正方形A₁B₁C₁C ，延长C₁B₁交x轴于点A₂ ，作正方形A₂B₂C₂C₁ ， …按这样的规律进行下去，第1个正方形的面积为；第n个正方形的面积为．

答案解析收藏纠错 + 选题
10. (2021九上·嘉祥期中) 同学们学习了线段的黄金分割之后，曾老师提出了一个新的定义：点C是线段AB上一点，若 $\text{[math]}$ ＝kn，则称点C为线段AB的“近A，n阶黄金分割点”．例如：若 $\text{[math]}$ ＝k₂ ，则称点C为线段AB的“近A，2阶黄金分割点”；若 $\text{[math]}$ ＝k₃ ，则称点C为线段AB的“近A，3阶黄金分割点”．若点C为线段AB的“近A，6阶黄金分割点”时，k₆＝．

答案解析收藏纠错 + 选题
11. (2023九上·东阿月考) 如图，已知△ABC中，D为边AC上一点，P为边AB上一点，AB=12，AC=8，AD=6，当AP的长度为时，△ADP和△ABC相似.

答案解析收藏纠错 + 选题
12. (2022九上·蚌山期中) 如图，在正方形网格中有三个三角形，分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中与 $\text{[math]}$ 相似的是．

答案解析收藏纠错 + 选题

三、解答题

13. (2023九上·罗湖月考) 如图，在菱形ABCD中，P是它对角线上面的一个点，连接CP后并延长，交CD于点E ，交BA的延长线于点F ．
1. （1）求证：∠DCP＝∠DAP；
2. （2）如果PE＝4，EF＝7，求线段PC的长．
答案解析收藏纠错 + 选题
14. (2023九上·资中期中) 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平，它的平面图可看作宽与长的比是 $\text{[math]}$ 的矩形，我们将这种宽与长的比是 $\text{[math]}$ 的矩形叫黄金矩形．如图①，已知黄金矩形 $\text{[math]}$ 的宽 $\text{[math]}$ ．
1. （1）黄金矩形 $\text{[math]}$ 的长 $\text{[math]}$ ；
2. （2）如图②，将图①中的黄金矩形裁剪掉一个以 $\text{[math]}$ 为边的正方形 $\text{[math]}$ ，得到新的矩形 $\text{[math]}$ ，猜想矩形 $\text{[math]}$ 是否为黄金矩形，并证明你的结论；
3. （3）在图②中，连接 $\text{[math]}$ ，求点 $\text{[math]}$ 到线段 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
15. (2023九上·郑州开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 边上的两个动点， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 相似吗？为什么？
2. （2）若 $\text{[math]}$ 即 $\text{[math]}$ 、 $\text{[math]}$ 重合 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ 时， $\text{[math]}$ ∽ $\text{[math]}$ ；
3. （3）当 $\text{[math]}$ 和 $\text{[math]}$ 满足怎样的数量关系时， $\text{[math]}$ ∽ $\text{[math]}$ ？请说明理由．
答案解析收藏纠错 + 选题
16. (2023九上·通榆期中) 再读教材：宽与长的比是 $\text{[math]}$ （约为0.618）的矩形叫做黄金矩形，黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形（提示：MN=2）．
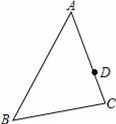
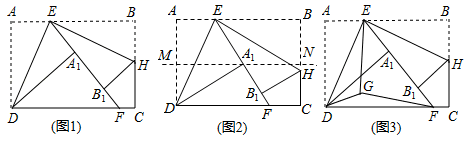
第－步：在矩形纸片一端利用图①的方法折出一个正方形，然后把纸片展平．
第二步：如图②，把这个正方形折成两个相等的矩形，再把纸片展平．
第三步：折出内侧矩形的对角线AB ，并把AB折到图③中所示的AD处．
第四步：展平纸片，按照所得的点D折出DE ，使DE⊥ND ，则图④中就会出现黄金矩形．
问题解决：
1. （1）图③中，AB=（保留根号）．
2. （2）如图③，判断四边形BADQ的形状，并说明理由．
3. （3）在图④中，直接写出所有黄金矩形．
答案解析收藏纠错 + 选题
17. (2019九上·丹东月考) 如图，△ABC 中，∠C=90°，AC=3cm，BC=4cm，动点 P 从点 B 出发以 2cm/s 速度向点C移动，同时动点 Q 从 C 出发以 1cm/s 的速度向点 A 移动，设它们的运动时间为 t.
1. （1）根据题意知：CQ=，CP=；（用含 t 的代数式表示）
2. （2） t 为何值时，△CPQ 的面积等于△ABC 面积的 $\text{[math]}$ ？
3. （3）运动几秒时，△CPQ 与△CBA 相似？
答案解析收藏纠错 + 选题
18. (2018九上·二道月考) 如图
1. （1）感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）
2. （2）探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．
3. （3）拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=6 $\text{[math]}$ ，CE=4，则DE的长为．
答案解析收藏纠错 + 选题
19. (2020九上·简阳月考) 如图1，矩形ABCD中，点E为AB边上的动点（不与A，B重合），把 $\text{[math]}$ 沿DE翻折，点A的对应点为 $\text{[math]}$ ，延长 $\text{[math]}$ 交直线DC于点F，再把 $\text{[math]}$ 折叠，使点B的对应点 $\text{[math]}$ 落在EF上，折痕EH交直线BC于点H.
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，直线MN是矩形ABCD的对称轴，若点 $\text{[math]}$ 恰好落在直线MN上，试判断 $\text{[math]}$ 的形状，并说明理由；
3. （3）如图3，在（2）的条件下，点G为 $\text{[math]}$ 内一点，且 $\text{[math]}$ ，试探究DG，EG，FG的数量关系.
答案解析收藏纠错 + 选题