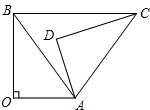


其中正确的结论是( )
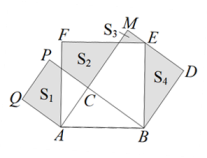






等腰直角三角形勾股高三角形(填“是”或“不是”);
如图②,为勾股高三角形,其中
为勾股顶点且
,
是
边上的高.试探究线段
与
的数量关系,并给予证明.
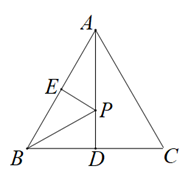
如图③,等腰三角形为勾股高三角形,其中
,
为
边上的高,过点
向
边引平行线与
边交于点
.若
, 试求线段
的长度.

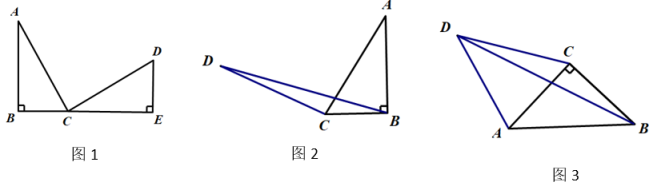
如图1,在△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=4,ED=3,则BE=.
如图2,在Rt△ABC中,∠ABC=90°,BC=3,过点C作CD⊥AC,且CD=AC,求△BCD的面积.
如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为14且CD的长为7,求△BCD的面积.


①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,若S△OBF:S△OCF=1:4,则BD的长为 ▲(直接写出所有结果).