人教版数学九年级全册知识点训练营——二次函数与一次函数

更新时间：2024-10-22 浏览次数：3 类型：复习试卷

一、夯实基础

1. (2023·碧江模拟) 将二次函数 $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位，再向上平移 $\text{[math]}$ 个单位后，顶点在直线 $\text{[math]}$ 上，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·霍邱月考) 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）

A . -4<x<3 B . x<-4 C . 3-<<x<-4 D . x>3或x<-4

答案解析收藏纠错 + 选题
3. (2019·无锡模拟) 如图，一次函数y=﹣x与二次函数为y=ax²+bx+c的图象相交于点M，N，则关于x的一元二次方程ax²+（b+1）x+c=0的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数 C . 没有实数根 D . 以上结论都正确

答案解析收藏纠错 + 选题
4. 不论m取何实数，抛物线y=2（x+m）²+m的顶点一定在下列哪个函数图象上（　　）

A . y=2x² B . y=-x C . y=-2x D . y=x

答案解析收藏纠错 + 选题
5. (2021·新吴模拟) 如图，二次函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ 和 $\text{[math]}$ ，则使不等式 $\text{[math]}$ 成立的x的取值范围是.

答案解析收藏纠错 + 选题
6. (2018九上·杜尔伯特期末) 抛物线y=x²+8x﹣4与直线x=﹣4的交点坐标是．

答案解析收藏纠错 + 选题
7. (2023九上·路桥月考) 已知二次函数y＝x²＋bx＋c经过A(1，1)和B(－1，－3)，二次函数与一次函数y＝－x－2交于C ， D两点．
1. （1）求二次函数的解析式．
2. （2）求三角形BCD的面积．
3. （3）结合图象直接写出不等式x²＋bx＋c＞－x－2的解集．
答案解析收藏纠错 + 选题
8. (2021·黄梅模拟) 绿色生态农场生产并销售某种有机产品，每日最多生产130kg，假设生产出的产品能全部售出，每千克的销售价y₁（元）与产量x（kg）之间满足一次函数关系y₁＝﹣ $\text{[math]}$ x+168，生产成本y₂（元）与产量x（kg）之间的函数图象如图中折线ABC所示.
1. （1）求生产成本y₂（元）与产量x（kg）之间的函数关系式；
2. （2）求日利润为W（元）与产量x（kg）之间的函数关系式；
3. （3）当产量为多少kg时，这种产品获得的日利润最大？最大日利润为多少元？
答案解析收藏纠错 + 选题

二、能力提升

9. (2024九上·杭州开学考) 二次函数 $\text{[math]}$ 和正比例函数 $\text{[math]}$ 的图象如图所示，则方程 $\text{[math]}$ 的两根之和（）

A . 大于 $\text{[math]}$ B . 等于 $\text{[math]}$ C . 小于 $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
10. (2024·牡丹江) 在平面直角坐标系中，抛物线y＝ax²+bx+c（a≠0）与x轴交于A、B两点，A（﹣3，0），B（1，0），与y轴交点C的纵坐标在﹣3～﹣2之间，根据图象判断以下结论：①abc²＞0；② $\text{[math]}$ ＜b＜2；③若 $\text{[math]}$ ﹣bx₁＝ $\text{[math]}$ ﹣bx₂且x₁≠x₂ ，则x₁+x₂＝﹣2；④直线y＝﹣ $\text{[math]}$ cx+c与抛物线y＝ax²+bx+c的一个交点（m ， n）（m≠0），则m＝ $\text{[math]}$ ．其中正确的结论是（）

A . ①②④ B . ①③④ C . ①②③ D . ①②③④

答案解析收藏纠错 + 选题
11. (2024·东坡模拟) 已知抛物线 $\text{[math]}$ 和直线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，其中 $\text{[math]}$ ，且满足 $\text{[math]}$ ，则直线 $\text{[math]}$ 一定经过（）

A . 第一、二象限 B . 第二、三象限 C . 第三、四象限 D . 第一、四象限

答案解析收藏纠错 + 选题
12. (2024九下·杭州开学考) 已知 $\text{[math]}$ .抛物线 $\text{[math]}$ 与线段BC至少有一个交点，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. 将二次函数 $\text{[math]}$ 在 $\text{[math]}$ 轴上方的图象沿 $\text{[math]}$ 轴翻折到 $\text{[math]}$ 轴下方，图象的其余部分不变，得到一个新图象．若直线 $\text{[math]}$ $\text{[math]}$ 与这个新图象有3个公共点，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ 或-12 B . $\text{[math]}$ 或2 C . -12或2 D . $\text{[math]}$ 或-12

答案解析收藏纠错 + 选题
14. (2024·凉山模拟) 当 $\text{[math]}$ 时，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 有交点，则a的取值范围是.

答案解析收藏纠错 + 选题
15. (2024九上·六安月考) 如图，点A在二次函数y＝ax²(a＞0)第一象限的图象上，AB⊥x轴，AC⊥y轴，垂足分别为B、C，连接BC，交函数图象于点D，DE⊥y轴于点E，则 $\text{[math]}$ 的值为..

答案解析收藏纠错 + 选题
16. (2024九上·黄石月考) 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点A(2，0)和点 $\text{[math]}$ ．
（1）求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
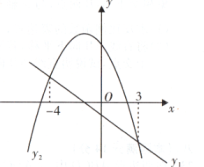
（2）求点 $\text{[math]}$ 的坐标，并结合图象写出不等式 $\text{[math]}$ 的解集；
（3）点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一个动点，将点 $\text{[math]}$ 向左平移 $\text{[math]}$ 个单位长度得到点 $\text{[math]}$ ，若线段 $\text{[math]}$ 与抛物线只有一个公共点，直接写出点 $\text{[math]}$ 的横坐标 $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题

三、拓展创新

17. (2024·嘉兴模拟) 已知直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 对称轴左侧部分的图象有且只有一个交点，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2024·旌阳模拟) 如图，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与x轴交于A ， B两点，与y轴交于点C ，其对称轴为直线 $\text{[math]}$ ，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ （ $\text{[math]}$ ）交于C ， D两点，且D为抛物线的顶点，则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④方程 $\text{[math]}$ 有两个不相等的实数根．其中结论正确的个数有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
19. (2024九上·曲周期末) 函数 $\text{[math]}$ 的图象与x轴交于点(2，0)，顶点坐标为(-1，n)，其中 $\text{[math]}$ ，以下结论正确的是（）
① $\text{[math]}$ ；

②函数 $\text{[math]}$ 在 $\text{[math]}$ 处的函数值相等；

③函数 $\text{[math]}$ 的图象与的函数 $\text{[math]}$ 图象总有两个不同的交点；

④函数 $\text{[math]}$ 在 $\text{[math]}$ 内既有最大值又有最小值．

A . ①③ B . ①②③ C . ①④ D . ②③④

答案解析收藏纠错 + 选题
20. (2023九上·随县期中) 抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是常数， $\text{[math]}$ ）的顶点坐标为 $\text{[math]}$ ，其中 $\text{[math]}$ ．下列四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 无实数解；④点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，若 $\text{[math]}$ ，则 $\text{[math]}$ ，能确定其正确的有（）个

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
21. (2024九上·吉安月考) 已知函数 $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ）， $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ），在同一平面直角坐标系中，若无论 $\text{[math]}$ 为何值，函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象总有公共点，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
22. (2023九上·梁子湖期中) 若一个点的纵坐标是横坐标的2倍，则称这个点为“倍值点”，如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都是“倍值点”，若关于x的二次函数 $\text{[math]}$ ， n为常数， $\text{[math]}$ 总有两个不同的倍值点，则n的取值范围是．

答案解析收藏纠错 + 选题
23. 如图，直线y= $\text{[math]}$ x+2与y轴交于点A，与直线y= $\text{[math]}$ x交于点B．以AB为边向右作菱形ABCD，点C恰好与原点O重合．抛物线y=(x-h)²+k的顶点在直线y= $\text{[math]}$ x上移动．若抛物线与菱形的边AB，BC都有公共点，则h的取值范围是

答案解析收藏纠错 + 选题
24. (2024九上·长沙开学考) 定义：在平面直角坐标系中，图形G上点P（x，y）的纵坐标y与其横坐标x的差y-x称为点P的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
（1）点A（2，6）的“坐标差”为________；
（2）求抛物线y=-x²+5.x+4的“特征值”；
（3）某二次函数y=-x²+bx+c（c≠0）的“特征值”为-1，点B与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等，求此二次函数的解析式；
（4）二次函数y=-x²+px+q的图象的顶点在“坐标差”为2的一次函数的图象上，四边形DEFO是矩形，点E的坐标为（7，3），点O为坐标原点，点D在x轴上点下在x轴上，当二次函数y=-x²+px+q的图象与矩形的边只有三个交点时，求此二次函数的解析式及特征值.

答案解析收藏纠错 + 选题