垂美四边形模型—北师大版数学八（上）知识点训练

更新时间：2024-10-27 浏览次数：4 类型：复习试卷

一、选择题

1. (2023八上·清苑期中) 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD ，对角线AC ， BD交于点O ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 15 B . 16 C . 17 D . 20

答案解析收藏纠错 + 选题

二、填空题

2. (2024八下·恩施期中) 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 $\text{[math]}$ ，对角线 $\text{[math]}$ 交于点O．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
3. (2024八上·雅安期末) 对角线互相垂直的四边形叫做“垂美”四边形，如图所示的“垂美”四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
4. (2024九下·泰山模拟) 小明学习了四边形后，对有特殊性质的四边形的探究产生了兴趣，发现了这样一类特殊的四边形：两条对角线互相垂直的四边形，叫做垂美四边形，如图：已知四边形 $\text{[math]}$ 中， $\text{[math]}$ ，垂足为 $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值等于．

答案解析收藏纠错 + 选题

三、实践探究题

5. (2024八下·高州期末) 定义：对角线互相垂直的四边形叫做“垂美”四边形．现有如图所示的“垂美”四边形 $\text{[math]}$ ，对角线 $\text{[math]}$ 相交于点O，若 $\text{[math]}$ ，求 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
6. (2024八下·平泉期中) 我们把对角线互相垂直的四边形称为“垂美四边形”，如图，已知四边形 $\text{[math]}$ ， $\text{[math]}$ ，像这样的四边形称为“垂美四边形”．
探索证明（1）如图，设 $\text{[math]}$ ，猜想 $\text{[math]}$ 之间的关系，用等式表示出来，并说明理由．（提示：运用勾股定理说理）
变式思考（2）如图， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ ，垂足为O，设 $\text{[math]}$ ，请用一个等式把 $\text{[math]}$ 三者之间的数量关系表示出来：
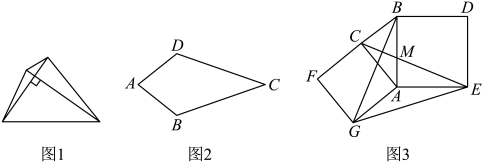
拓展应用（3）如图，在矩形 $\text{[math]}$ 中，E为 $\text{[math]}$ 的中点，若四边形 $\text{[math]}$ 为“垂美四边形”，且 $\text{[math]}$ 求 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
7. (2024八下·梁平月考) 我们把对角线互相垂直的四边形称为“垂美四边形”．如图1，已知四边形 $\text{[math]}$ ， $\text{[math]}$ ，像这样的四边形称为“垂美四边形”．
1. （1）探索证明
  如图1，设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，猜想 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的关系，用等式表示出来，并说明你的理由．
2. （2）变式思考
  如图2， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ ，垂足为O ， $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请用一个等式把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三者之间的数量关系表示出来：．
3. （3）拓展应用
  如图3，在长方形 $\text{[math]}$ 中，E为 $\text{[math]}$ 的中点，若四边形 $\text{[math]}$ 为“垂美四边形”，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
8. (2023八下·安化期末) 如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
1. （1）概念理解：我们已经学习了平行四边形、菱形、矩形、正方形，在这四种图形中是垂美四边形的是．
2. （2）性质探究：如图2，已知四边形 $\text{[math]}$ 是垂美四边形，求证： $\text{[math]}$ ．
3. （3）问题解决：如图3，分别以 $\text{[math]}$ 的直角边 $\text{[math]}$ 和斜边 $\text{[math]}$ 为边向外作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题