

数学课上,老师出示了这样一道题:
如图1,△ABC中,AC=BC=a,∠ACB=90°,点D在AB上,且AD=kAB(其中0<k< ),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现DC与DE相等”;
小伟:“通过构造全等三角形,经过进一步推理,可以得到DC与DE相等”
小强:“通过进一步的推理计算,可以得到BE与BC的数量关系”
老师:“保留原题条件,连接CE交AB于点O.如果给出BO与DO的数量关系,那么可以求出CO•EO的值”



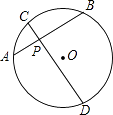
已知:如图①,过 外一点
作
的两条割线,一条交
于
、
点,另一条交
于
、
点.
求证: .
证明一:连接 、
,
∵ 和
为
所对的圆周角,∴_▲_.
又∵ ,∴_▲_,∴_▲_.
即 .
研究后发现,如图②,如果连接 、
,即可得到学习过的圆内接四边形
.那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.
证明二:连接 、
,