
①的长可以为
;
②当农场面积为
时,满足条件的
的长只有一个值;
③农场面积的最大值为
;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过 .
其中,正确结论的是.(只需填序号)





(1)求此抛物线的解析式;
(2)如图1,连接 , 求
面积的最大值及此时点P的坐标;
(3)如图2,连接 , 过点P作
于点E,是否存在点P使以P,D,E三点为顶点的三角形与
相似,若存在,直接写出点P的坐标;若不存在,请说明理由.


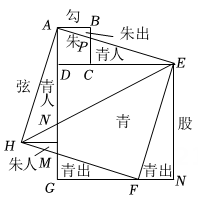

(1)若 ,
, 则
的长是cm.
(2)若 , 则
的值是.
素材一 | 如图,在 |
|
素材二 | 如图,在 |
|
素材三 | 如图,矩形 |
|
任务一 | 若素材一中的 | |
任务二 | 若素材二中的 | |
任务三 | 若任务二中的 |
|
任务四 | 若任务二中的 | |
任务五 | 当素材三中的实验室“可利用比”最高,求此时 |