浙江省宁波市象山县2019届九年级下学期数学3月月考试卷

更新时间：2024-07-13 浏览次数：396 类型：月考试卷

一、单选题

1. (2019九下·象山月考) “367 人中有 2 人同月同日生”这一事件是（）

A . 随机事件 B . 必然事件 C . 不可能事件 D . 确定事件

答案解析收藏纠错 + 选题
2. (2022八上·翁源期中) 如果n边形的内角和是它外角和的4倍，则n等于（）

A . 7 B . 8 C . 10 D . 9

答案解析收藏纠错 + 选题
3. (2019·赤峰模拟) 在平面直角坐标系xOy中，若点P（4，3）在⊙O内，则⊙O的半径r的取值范围是（）

A . 0＜r＜4 B . 3＜r＜4 C . 4＜r＜5 D . r＞5

答案解析收藏纠错 + 选题
4. (2021九上·顺义月考) 如图，在△ABC中，点D，E分别为边AB，AC上的点，且DE∥BC．若AD＝5，BD＝10，AE＝3，则CE的长为（）

A . 3 B . 6 C . 9 D . 12

答案解析收藏纠错 + 选题
5. (2019九下·象山月考) 如图，一根6m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动）那么小羊A在草地上的最大活动区域面积是（）

A . 9πm² B . $\text{[math]}$ πm² C . 15πm² D . $\text{[math]}$ πm²

答案解析收藏纠错 + 选题
6. (2022九上·汽开区期末) 下列命题是真命题的是（）

A . 直径是圆中最长的弦 B . 三个点确定一个圆 C . 平分弦的直径垂直于弦 D . 相等的圆心角所对的弦相等

答案解析收藏纠错 + 选题
7. (2020九上·郑州月考) 如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（）

A . 28cm² B . 27cm² C . 21cm² D . 20cm²

答案解析收藏纠错 + 选题
8. (2021九上·高坪月考) 已知（﹣1，y₁），（2，y₂），（3，y₃）在二次函数y＝﹣x²+4x+c的图象上，则y₁ ， y₂ ， y₃的大小关系正确的是（）

A . y₁＜y₂＜y₃ B . y₃＜y₂＜y₁ C . y₃＜y₁＜y₂ D . y₁＜y₃＜y₂

答案解析收藏纠错 + 选题
9. (2019·信阳模拟) 如图，AB是⊙O的直径，点C，D在⊙O上，且点C，D在AB的异侧，连接AD，BD，OD，OC，若∠ABD＝15°，且AD∥OC，则∠BOC的度数为（）

A . 120° B . 105° C . 100° D . 110°

答案解析收藏纠错 + 选题
10. (2019九下·象山月考) 已知二次函数y＝ax²+bx+c（a≠0）的图象如图，则下列结论错误的是（）

A . 4a+2b+c＞0 B . abc＜0 C . b＜a﹣c D . 3b＞2c

答案解析收藏纠错 + 选题
11. (2019九下·象山月考) 如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，点D为边BC的中点，点M为边AB上的一动点，点N为边AC上的一动点，且∠MDN＝90°，则sin∠DMN为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019九下·象山月考) 如图，在Rt△ABC中，BC＝3，∠BAC＝30°，斜边AB的两个端点分别在相互垂直的射线OM，ON上滑动．下列结论：①若C、O两点关于AB对称，则OA＝3 $\text{[math]}$ ；②若AB平分CO，则AB⊥CO；③C，O两点间的最大距离是6；④斜边AB的中点D运动的路径长是 $\text{[math]}$ π，其中正确的有（）

A . ①② B . ③④ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题

二、填空题

13. (2023九上·历城月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
14. (2024九下·龙湖模拟) 在一个不透明的布袋中装有4个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到白球的概率是 $\text{[math]}$ ，则n＝．

答案解析收藏纠错 + 选题
15. (2019九下·盐都月考) 把抛物线y＝﹣（x﹣2）²﹣2先向左平移1个单位，再向下平移1个单位，得到的抛物线的解析式为。

答案解析收藏纠错 + 选题
16. (2019九下·象山月考) 如图，四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，∠BCD＝130°，则∠ABD的度数是．

答案解析收藏纠错 + 选题
17. (2022九上·虹口期中) 如图，将矩形ABCD绕点A按逆时针方向旋转一定角度后，BC的对应边B′C交CD边于点G，如果当AB′＝B′G时量得AD＝7，CG＝4，连接BB′、CC′，那么 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
18. (2019九下·象山月考) 如图，⊙O过M点，⊙M交⊙O于A，延长⊙O的直径AB交⊙M于C，若AB＝8，BC＝1，则AM＝．

答案解析收藏纠错 + 选题

三、解答题

19. (2019九上·东城期中) 计算：2cos30°﹣tan60°+sin30°+ $\text{[math]}$ tan45°．

答案解析收藏纠错 + 选题

20. (2019九下·象山月考) 王老师将 $\text{[math]}$ 个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．

摸球的次数 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
摸到黑球的次数 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
摸到黑球的频率 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（1）补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是（精确到0.01）；
（2）估算袋中白球的个数；
（3）在 $\text{[math]}$ 的条件下，若小强同学有放回地连续两次摸球，用画树状图或列表的方法计算他两次都摸出白球的概率．

答案解析收藏纠错 + 选题

21. (2019九上·上街期末) 如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15m，CD=20m．AB和CD之间有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上．求两幢建筑物之间的距离BD．（结果精确到0.1m）（参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90）

答案解析收藏纠错 + 选题
22. (2018九上·浙江期中) 如图，一圆弧形钢梁
1. （1）请用直尺和圆规补全钢梁所在圆
2. （2）若钢梁的拱高为8米，跨径为40米，求这钢梁圆弧的半径。
答案解析收藏纠错 + 选题
23. (2022九上·奉贤期中) 如图，已知菱形ABCD，点E是AB的中点，AF⊥BC于点F，联结EF、ED、DF，DE交AF于点G，且AE²＝EG•ED．
1. （1）求证：DE⊥EF；
2. （2）求证：BC²＝2DF•BF．
答案解析收藏纠错 + 选题
24. (2019九下·象山月考) 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．
1. （1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；
2. （2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
答案解析收藏纠错 + 选题
25. (2019九下·象山月考) 如图所示，已知抛物线y＝﹣x²+bx+c与x轴相交于A、B两点，且点A的坐标为（1，0），与y轴交于点C，对称轴直线x＝2与x轴相交于点D，点P是抛物线对称轴上的一个动点，以每秒1个单位长度的速度从抛物线的顶点E向下运动，设点P运动的时间为t（s）．
1. （1）点B的坐标为，抛物线的解析式是；
2. （2）求当t为何值时，△PAC的周长最小？
3. （3）当t为何值时，△PAC是以AC为腰的等腰三角形？
答案解析收藏纠错 + 选题
26. (2019九下·象山月考) 定义：若一个四边形能被其中的一条对角线分割成两个相似三角形，则称这个四边形为“友谊四边形”．我们熟知的平行四边形就是“友谊四边形”，
1. （1）如图1，在4×4的正方形网格中有一个Rt△ABC，请你在网格中找格点D，使得四边形ABCD是被AC分割成的“友谊四边形”，（要求画出点D的2种不同位置）
2. （2）如图2，BD平分∠ABC，BD＝4 $\text{[math]}$ ，BC＝8，四边形ABCD是被BD分割成的“友谊四边形”，求AB长；
3. （3）如图3，圆内接四边形ABCD中，∠ABC＝60，点E是 $\text{[math]}$ 的中点，连结BE交CD于点F，连结AF，∠DAF＝30°
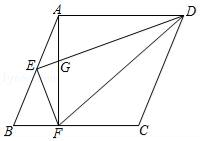
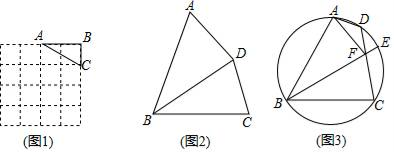
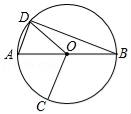
  ①求证：四边形ABCF是“友谊四边形”；
  ②若△ABC的面积为6 $\text{[math]}$ ，求线段BF的长．
答案解析收藏纠错 + 选题