2019年高考数学真题试卷（江苏卷）

更新时间：2021-05-20 浏览次数：1499 类型：高考真卷

一、填空题：本大题共14小题，每小题5分，共计70分．

1. (2019·江苏) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
2. (2019·江苏) 已知复数 $\text{[math]}$ 的实部为0，其中 $\text{[math]}$ 为虚数单位，则实数a的值是.

答案解析收藏纠错 + 选题
3. (2019·江苏) 下图是一个算法流程图，则输出的S的值是.

答案解析收藏纠错 + 选题
4. (2023高一上·衡水期中) 函数 $\text{[math]}$ 的定义域是.

答案解析收藏纠错 + 选题
5. (2023高二下·简阳月考) 已知一组数据6，7，8，8，9，10，则该组数据的方差是.

答案解析收藏纠错 + 选题
6. (2024高一下·柳州月考) 从3名男同学和2名女同学中任选2名同学参加志愿者服务，则选出的2名同学中至少有1名女同学的概率是.

答案解析收藏纠错 + 选题
7. (2019·江苏) 在平面直角坐标系 $\text{[math]}$ 中，若双曲线 $\text{[math]}$ 经过点（3，4)，则该双曲线的渐近线方程是.

答案解析收藏纠错 + 选题
8. (2019·江苏) 已知数列 $\text{[math]}$ 是等差数列， $\text{[math]}$ 是其前n项和.若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
9. (2022高一下·阳信期中) 如图，长方体 $\text{[math]}$ 的体积是120，E为 $\text{[math]}$ 的中点，则三棱锥E-BCD的体积是.

答案解析收藏纠错 + 选题
10. (2019高二上·上杭月考) 在平面直角坐标系 $\text{[math]}$ 中，P是曲线 $\text{[math]}$ 上的一个动点，则点P到直线x+y=0的距离的最小值是.

答案解析收藏纠错 + 选题
11. (2019·江苏) 在平面直角坐标系 $\text{[math]}$ 中，点A在曲线y=lnx上，且该曲线在点A处的切线经过点（-e，-1)(e为自然对数的底数），则点A的坐标是.

答案解析收藏纠错 + 选题
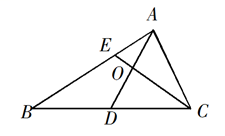
12. (2019·江苏) 如图，在 $\text{[math]}$ 中，D是BC的中点，E在边AB上，BE=2EA ， AD与CE交于点 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
13. (2021高一上·舒城期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2019高三上·北京月考) 设 $\text{[math]}$ 是定义在R上的两个周期函数， $\text{[math]}$ 的周期为4， $\text{[math]}$ 的周期为2，且 $\text{[math]}$ 是奇函数.当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ，其中k>0.若在区间(0，9]上，关于x的方程 $\text{[math]}$ 有8个不同的实数根，则k的取值范围是.

答案解析收藏纠错 + 选题

二、解答题：本大题共6小题，共计90分．

15. (2019·江苏) 在△ABC中，角A ， B ， C的对边分别为a ， b ， c ．
1. （1）若a=3c ， b= $\text{[math]}$ ，cosB= $\text{[math]}$ ，求c的值；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
16. (2022高一下·伊犁期末) 如图，在直三棱柱ABC－A₁B₁C₁中，D ， E分别为BC ， AC的中点，AB=BC ．

求证：
1. （1） A₁B₁∥平面DEC₁；
2. （2） BE⊥C₁E ．
答案解析收藏纠错 + 选题
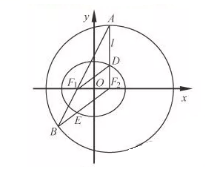
17. (2019·江苏) 如图，在平面直角坐标系xOy中，椭圆C： $\text{[math]}$ 的焦点为F₁（–1、0），F₂（1，0）．过F₂作x轴的垂线l ，在x轴的上方，l与圆F₂： $\text{[math]}$ 交于点A ，与椭圆C交于点D.连结AF₁并延长交圆F₂于点B ，连结BF₂交椭圆C于点E ，连结DF₁ ．已知DF₁= $\text{[math]}$ ．
1. （1）求椭圆C的标准方程；
2. （2）求点E的坐标．
答案解析收藏纠错 + 选题
18. (2019高三上·海南月考) 如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l ，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q ，并修建两段直线型道路PB、QA ．规划要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位：百米）．
1. （1）若道路PB与桥AB垂直，求道路PB的长；
2. （2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；
3. （3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．
答案解析收藏纠错 + 选题
19. (2020高三上·绵阳月考) 设函数 $\text{[math]}$ 、 $\text{[math]}$ 为f（x）的导函数．
1. （1）若a=b=c ， f（4）=8，求a的值；
2. （2）若a≠b ， b=c ，且f（x）和 $\text{[math]}$ 的零点均在集合 $\text{[math]}$ 中，求f（x）的极小值；
3. （3）若 $\text{[math]}$ ，且f（x）的极大值为M ，求证:M≤ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2019·江苏) 定义首项为1且公比为正数的等比数列为“M－数列”.
1. （1）已知等比数列{a_n} $\text{[math]}$ 满足： $\text{[math]}$ ，求证：数列{a_n}为“M－数列”；
2. （2）已知数列{b_n}满足： $\text{[math]}$ ，其中S_n为数列{b_n}的前n项和．
  ①求数列{b_n}的通项公式；
  
  ②设m为正整数，若存在“M－数列”{c_n} $\text{[math]}$ ，对任意正整数k ，当k≤m时，都有 $\text{[math]}$ 成立，求m的最大值．
答案解析收藏纠错 + 选题

三、数学Ⅱ(附加题)（每题10分）【选做题】本题包括21、22、23三题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．

21. (2019·江苏) A.[选修4-2：矩阵与变换]
已知矩阵 $\text{[math]}$
1. （1）求A²；
2. （2）求矩阵A的特征值.
答案解析收藏纠错 + 选题
22. (2019·江苏) 在极坐标系中，已知两点 $\text{[math]}$ ，直线l的方程为 $\text{[math]}$ .
1. （1）求A ， B两点间的距离；
2. （2）求点B到直线l的距离.
答案解析收藏纠错 + 选题
23. (2019·江苏) 设 $\text{[math]}$ ，解不等式 $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、【必做题】第24题、第25题，每题10分，共计20分．

24. (2020高二下·武汉期中) 设 $\text{[math]}$ .已知 $\text{[math]}$ .
1. （1）求n的值；
2. （2）设 $\text{[math]}$ ，其中 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2019·江苏) 在平面直角坐标系xOy中，设点集 $\text{[math]}$ ， $\text{[math]}$
令 $\text{[math]}$ .从集合M_n中任取两个不同的点，用随机变量X表示它们之间的距离.
1. （1）当n=1时，求X的概率分布；
2. （2）对给定的正整数n（n≥3），求概率P（X≤n）（用n表示）.
答案解析收藏纠错 + 选题