 B .
B . 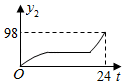 C .
C . 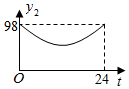 D .
D . 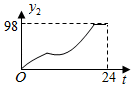

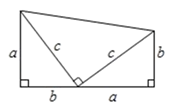
如图,两个边长分别为 、
、
的直角三角形和一个两条直角边都是
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;

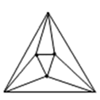
边形有
个顶点,在它的内部再画
个点,以(
)个点为顶点,把
边形剪成若干个三角形,设最多可以剪得
个这样的三角形.当
,
时,如图,最多可以剪得
个这样的三角形,所以
.
①当 ,
时,如图,
;当
,
时,
;
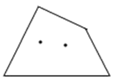
②对于一般的情形,在 边形内画
个点,通过归纳猜想,可得
(用含
、
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
①半径为 的圆:;
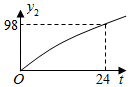
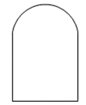
②如图,上方是半径为 的半圆,下方是正方形的三条边的“窗户形“:;
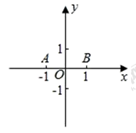
①若 ,用直尺和圆规画出点
所在的区域并求它的面积(所在区域用阴影表示);
②若点 在⊙
上运动,⊙
的半径为
,圆心
在过点
且与
轴垂直的直线上.对于⊙
上任意点
,都有
,直接写出圆心
的横坐标
的取值范围.