初中数学浙教版九年级上册1.4 二次函数的应用强化提升训练

更新时间：2019-08-22 浏览次数：488 类型：同步测试

一、综合训练

1. 二次函数y=ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x₁和x₂ ，且x₁＜x₂ ，则﹣5＜x₁＜x₂＜1；④若方程|ax²+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2019九上·余杭月考) 四位同学在研究函数y₁＝ax²＋ax－2a (a是非零常数)时，甲发现该函数图象总经过定点；乙发现若抛物线y₁＝ax²＋ax－2a总不经过点P(x₀－3，x₀²－16)，则符合条件的点P有且只有2个；丙发现若直线y₂＝kx＋b与函数y₁交于x轴上同一点，则b＝－k；丁发现若直线y₃＝m (m≠0)与抛物线有两个交点(x₁ ， y₁)(x₂ ， y₂)，则x₁＋x₂＋1＝0.已知这四位同学中只有一位发现的结论是错误的，则该同学是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
3. (2022·广汉模拟) 如图，已知抛物线y＝﹣x²+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．
1. （1）求抛物线及直线AC的函数关系式；
2. （2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；
3. （3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
4. 已知y是关于x的函数，若其函数图象经过点P（t，t），则称点P为函数图象上的“bingo点”，例如：y＝2x﹣1上存在“bingo点”P（1，1）
1. （1）直线（填写直线解析式）上的每一个点都是“bingo点”；双曲线y＝ $\text{[math]}$ 上的“bingo点”是。
2. （2）若抛物线y＝ $\text{[math]}$ x²+（ $\text{[math]}$ a+1）x﹣ $\text{[math]}$ a²﹣a+2上有“bingo点”，且“bingo点”A、B（点A和点B可以重合）的坐标为A（x₁ ， y₁），B（x₂ ， y₂），求x₁²+x₂²的最小值
3. （3）若函数y＝ $\text{[math]}$ x²+（n﹣k+1）x+m+k﹣1的图象上存在唯一的一个“bingo点”，且当﹣2≤n≤1时，m的最小值为k，求k的值．
答案解析收藏纠错 + 选题
5. 如图
1. （1）【探索发现】
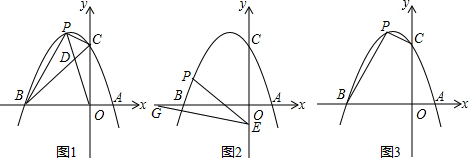
  如图①，是一张直角三角形纸片，∠B＝90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为．
2. （2）【拓展应用】
  如图②，在△ABC中，BC＝a，BC边上的高AD＝h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为．（用含a，h的代数式表示）
3. （3）【灵活应用】
  如图③，有一块“缺角矩形”ABCDE，AB＝30，BC＝40，AE＝20，CD＝16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．
答案解析收藏纠错 + 选题
6. (2019九下·秀洲月考) 嘉兴素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．
1. （1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；
2. （2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为 $\text{[math]}$ ；y与t的函数关系如图所示．
  ①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；
  
  ②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额﹣总成本）
答案解析收藏纠错 + 选题
7. (2019九下·象山月考) 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．
1. （1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；
2. （2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
答案解析收藏纠错 + 选题
8. (2018九上·新乡期末) 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y＝a（x﹣4）²+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．
1. （1）当a＝﹣ $\text{[math]}$ 时，①求h的值；②通过计算判断此球能否过网．
2. （2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为 $\text{[math]}$ m的Q处时，乙扣球成功，求a的值．
答案解析收藏纠错 + 选题
9. (2019九上·腾冲期末) 在平面直角坐标系中，已知抛物线y＝ax²+bx﹣4经过A（﹣4，0），C（2，0）两点．
1. （1）求抛物线的解析式；
2. （2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值；
3. （3）若点P是抛物线上的动点，点Q是直线y＝﹣x上的动点，点B是抛物线与y轴交点．判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
答案解析收藏纠错 + 选题

二、中考演练

10. (2019·荆州) 若二次函数 $\text{[math]}$ 图象的顶点在一次函数 $\text{[math]}$ 的图象上，则称 $\text{[math]}$ 为 $\text{[math]}$ 的伴随函数，如： $\text{[math]}$ 是 $\text{[math]}$ 的伴随函数.
1. （1）若 $\text{[math]}$ 是 $\text{[math]}$ 的伴随函数，求直线 $\text{[math]}$ 与两坐标轴围成的三角形的面积；
2. （2）若函数 $\text{[math]}$ 的伴随函数 $\text{[math]}$ 与 $\text{[math]}$ 轴两个交点间的距离为4，求 $\text{[math]}$ ， $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
11. (2019·北部湾) 如图抛物线C₁的顶点在抛物线C₂上，抛物线C₂的顶点也在抛物线C₁上时.那么我们称抛物线C₁与C₂“互为关联”的抛物线.如图1，已知抛物线C₁：y₁= $\text{[math]}$ x²+x与C₂：y₂=ax²+x+c是“互为关联”的抛物线，点A，B分别是抛物线C₁ ， C₂的顶点，抛物线C₂经过点D(6，-1).
1. （1）直接写出A，B的坐标和抛物线C₂的解析式：
2. （2）抛物线C₂上是否存在点E，使得△ABE是直角三角形?如果存在.请求出点E的坐标；如果不存在，请说明理由：
3. （3）如图2.点F(-6，3)在抛物线C₁上，点M、N分别是抛物线C₁ ， C₂上的动点，且点M，N的横坐标相同，记△AFM面积为S₁(当点M与点A，F重合时S₁=0)，△ABN的面积为S₂(当点N与点A，B重合时，S₂=0)，令S=S₁+S₂.观察图像.当y₁≤y₂时，写出x的取值范围.并求出在此范围内S的最大值.
答案解析收藏纠错 + 选题
12. (2018·日照) 在平面直角坐标系中，我们把横、纵坐标均为整数的点叫做整点．已知反比例函数y= $\text{[math]}$ （m＜0）与y=x²﹣4在第四象限内围成的封闭图形（包括边界）内的整点的个数为2，则实数m的取值范围为．

答案解析收藏纠错 + 选题
13. (2019九上·绵阳期中) 如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（）

A . 18m² B . $\text{[math]}$ m² C . $\text{[math]}$ m² D . $\text{[math]}$ m²

答案解析收藏纠错 + 选题
14. (2020九上·瑶海月考) 我市某超市销售一种文具，进价为5元/件.售价为6元/件时，当天的销售量为100件.在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件.设当天销售单价统一为x元/件（x≥6，且x是按0.5元的倍数上涨），当天销售利润为y元.
1. （1）求y与x的函数关系式（不要求写出自变量的取值范围）；
2. （2）要使当天销售利润不低于240元，求当天销售单价所在的范围；
3. （3）若每件文具的利润不超过80%，要想当天获得利润最大，每件文具售价为多少元？并求出最大利润.
答案解析收藏纠错 + 选题
15. (2021九上·乐清月考) 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（）

A . 此抛物线的解析式是y=﹣ $\text{[math]}$ x²+3.5 B . 篮圈中心的坐标是（4，3.05） C . 此抛物线的顶点坐标是（3.5，0） D . 篮球出手时离地面的高度是2m

答案解析收藏纠错 + 选题
16. (2019·黔东南) 已知抛物线y=ax²+bx+3经过点A(1，0)和点B(-3，0)，与y轴交于点C，点P为第二象限内抛物线上的动点.
1. （1）抛物线的解析式为，抛物线的顶点坐标为；
2. （2）如图1，连接OP交BC于点D，当S_△CPD：S_△BPD=1：2时，请求出点D的坐标；
3. （3）如图2，点E的坐标为(0，-1)，点G为x轴负半轴上的一点，∠OGE=15°，连接PE，若∠PEG=2∠OGE，请求出点P的坐标；
4. （4）如图3，是否存在点P，使四边形BOCP的面积为8?若存在，请求出点P的坐标；若不存在，请说明理由
答案解析收藏纠错 + 选题