浙江省台州市临海市2020届九年级上学期数学期末考试试卷

更新时间：2020-05-29 浏览次数：439 类型：期末考试

一、选择题（共10小题）

1. (2020九上·临海期末) 以下四个图形中，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020九上·临海期末) 若关于x的一元二次方程x²+2x﹣m＝0的一个根是x＝1，则m的值是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2020九上·龙岗期中) 某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图，则符合这一结果的试验可能是（）

A . 抛一枚硬币，出现正面朝上 B . 掷一个正六面体的骰子，出现3点朝上 C . 任意画一个三角形，其内角和是360° D . 从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球

答案解析收藏纠错 + 选题
4. (2020九上·临海期末) 如图，PA、PB分别与⊙O相切于A、B两点，点C为⊙O上一点，连AC、BC，若∠P＝80°，则的∠ACB度数为（）

A . 40° B . 50° C . 60° D . 80°

答案解析收藏纠错 + 选题
5. (2024九上·遵义月考) 电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事，一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把增长率记作x，则方程可以列为（）

A . 3（1+x）＝10 B . 3（1+x）²＝10 C . 3+3（1+x）²＝10 D . 3+3（1+x）+3（1+x）²＝10

答案解析收藏纠错 + 选题
6. (2020·无锡模拟) 用一个半径为15、圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是（）

A . 5 B . 10 C . 5π D . 10π

答案解析收藏纠错 + 选题
7. (2020九上·临海期末) 如图，正比例函数y＝x与反比例函数y＝ $\text{[math]}$ 的图象相交于A，C两点．AB⊥x轴于B，CD⊥x轴于D，当四边形ABCD的面积为6时，则k的值是（）

A . 6 B . 3 C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·新昌期中) 若抛物线y＝x²+bx+c与x轴只有一个公共点，且过点A（m，n），B（m﹣8，n），则n的值为（）

A . 8 B . 12 C . 15 D . 16

答案解析收藏纠错 + 选题
9. (2020九上·临海期末) 如图，在正方形ABCD中，AB＝5，点M在CD的边上，且DM＝2，△AEM与△ADM关于AM所在的直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·临海期末) 已有甲、乙、丙三人，甲说乙在说谎，乙说丙在说谎，丙说甲和乙都在说谎，则（）

A . 甲说实话，乙和丙说谎 B . 乙说实话，甲和丙说谎 C . 丙说实话，甲和乙说谎 D . 甲、乙、丙都说谎

答案解析收藏纠错 + 选题

二、填空题（共6小题）

11. (2020九上·临海期末) 若反比例函数的图象经过点（2，﹣2），（m，1），则m＝．

答案解析收藏纠错 + 选题
12. (2020九上·临海期末) 如图，在等腰直角△ABC中，∠C＝90°，将△ABC绕顶点A逆时针旋转80°后得到△AB′C′，则∠CAB′的度数为．

答案解析收藏纠错 + 选题
13. (2023八下·石景山期末) 已知（a+b）（a+b﹣4）＝﹣4，那么（a+b）＝．

答案解析收藏纠错 + 选题
14. (2023九上·椒江期中) 某班从三名男生（含小强）和五名女生中，选四名学生参加学校举行的“中华古诗文朗诵大赛”，规定女生选n名，若男生小强参加是必然事件，则n＝．

答案解析收藏纠错 + 选题
15. (2020九上·临海期末) 如图，已知等边△ABC的边长为4，P是AB边上的一个动点，连接CP，过点P作∠EPC＝60°，交AC于点E，以PE为边作等边△EPD，顶点D在线段PC上，O是△EPD的外心，当点P从点A运动到点B的过程中，点O也随之运动，则点O经过的路径长为．

答案解析收藏纠错 + 选题
16. (2020九上·椒江期中) 扫地机器人能够自主移动并作出反应，是因为它发射红外信号反射回接收器，机器人在打扫房间时，若碰到障碍物则发起警报．若某一房间内A、B两点之间有障碍物，现将A、B两点放置于平面直角坐标系xOy中（如图），已知点A，B的坐标分别为（0，4），（6，4），机器人沿抛物线y＝ax²﹣4ax﹣5a运动．若机器人在运动过程中只触发一次报警，则a的取值范围是．

答案解析收藏纠错 + 选题

三、解答题（共8小题）

17. (2020九上·临海期末) 已知二次函数y＝2x²+4x+3，当﹣2≤x≤﹣1时，求函数y的最小值和最大值，如图是小明同学的解答过程．你认为他做得正确吗？如果正确，请说明解答依据，如果不正确，请写出你得解答过程．

答案解析收藏纠错 + 选题
18. (2021九上·寻乌期末) 某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m， $\text{[math]}$ 分别用 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 表示 $\text{[math]}$ ；田赛项目：跳远，跳高 $\text{[math]}$ 分别用 $\text{[math]}$ 、 $\text{[math]}$ 表示 $\text{[math]}$ .
1. （1）该同学从5个项目中任选一个，恰好是田赛项目的概率为；
2. （2）该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率.
答案解析收藏纠错 + 选题
19. (2019九上·兴国期中) 如图，AB、AD是⊙O的弦，△ABC是等腰直角三角形，△ADC≌△AEB，请仅用无刻度直尺作图：
1. （1）在图1中作出圆心O；
2. （2）在图2中过点B作BF∥AC．
答案解析收藏纠错 + 选题
20. (2020九上·临海期末) “十一”黄金周期间，我市享有“江南八达岭”美誉的江南长城旅游区，为吸引游客组团来此旅游，特推出了如下门票收费标准：
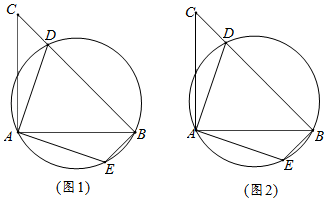
标准一：如果人数不超过20人，门票价格60元/人；

标准二：如果人数超过20人，每超过1人，门票价格降低2元，但门票价格不低于50元/人．
1. （1）若某单位组织23名员工去江南长城旅游区旅游，购买门票共需费用多少元？
2. （2）若某单位共支付江南长城旅游区门票费用共计1232元，试求该单位这次共有多少名员工去江南长城旅游区旅游？
答案解析收藏纠错 + 选题
21. (2020九上·临海期末) 如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且 $\text{[math]}$ ，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．
1. （1）证明：GF是⊙O的切线；
2. （2）若AG＝6，GE＝6 $\text{[math]}$ ，求⊙O的半径．
答案解析收藏纠错 + 选题
22. (2020九上·临海期末) 如图1，直线y＝x与双曲线y＝ $\text{[math]}$ 交于A，B两点，根据中心对称性可以得知OA＝OB．
1. （1）如图2，直线y＝2x+1与双曲线y＝ $\text{[math]}$ 交于A，B两点，与坐标轴交点C，D两点，试证明：AC＝BD；
2. （2）如图3，直线y＝ax+b与双曲线y＝ $\text{[math]}$ 交于A，B两点，与坐标轴交点C，D两点，试问：AC＝BD还成立吗？
3. （3）如果直线y＝x+3与双曲线y＝ $\text{[math]}$ 交于A，B两点，与坐标轴交点C，D两点，若DB+DC≤5 $\text{[math]}$ ，求出k的取值范围．
答案解析收藏纠错 + 选题
23. (2020九上·临海期末) 已知抛物线y＝x²﹣bx+2b（b是常数）．
1. （1）无论b取何值，该抛物线都经过定点 D．请写出点D的坐标．
2. （2）该抛物线的顶点是（m，n），当b取不同的值时，求n关于m的函数解析式．
3. （3）若在0≤x≤4的范围内，至少存在一个x的值，使y＜0，求b的取值范围．
答案解析收藏纠错 + 选题
24. (2020九上·临海期末) 如图1：在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），试探索AD，BD，CD之间满足的等量关系，并证明你的结论．
小明同学的思路是这样的：将线段AD绕点A逆时针旋转90°，得到线段AE，连接EC，DE．继续推理就可以使问题得到解决．
1. （1）请根据小明的思路，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
2. （2）如图2，在Rt△ABC中，AB＝AC，D为△ABC外的一点，且∠ADC＝45°，线段AD，BD，CD之间满足的等量关系又是如何的，请证明你的结论；
3. （3）如图3，已知AB是⊙O的直径，点C，D是⊙O上的点，且∠ADC＝45°．
  ①若AD＝6，BD＝8，求弦CD的长为；
  
  ②若AD+BD＝14，求 $\text{[math]}$ 的最大值，并求出此时⊙O的半径．
答案解析收藏纠错 + 选题