北京市平谷县杨桥中学2019年中考数学二模考试试卷

更新时间：2020-04-23 浏览次数：197 类型：中考模拟

一、选择题（本题共16分，每小题2分）第1-8题均有四个选。正确选项只有一个．

1. (2023八上·灞桥开学考) 甲骨文是我国古代的一种文字，是汉字的早期形式，反映了我国悠久的历史文化，体现了我国古代劳动人民的智慧，下列甲骨文中，不是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019·北京模拟) 如图，数轴上的点A所表示的数为x，则x的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ +1 C . $\text{[math]}$ ﹣1 D . 1﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019·北京模拟) 如图，七边形ABCDEFG中，AB、ED的延长线交于点O，着∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（　　）

A . 30° B . 35° C . 40° D . 45°

答案解析收藏纠错 + 选题
4. (2021七上·蒙阴期末) 近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片．现在中国高速铁路营运里程将达到22000公里，将22000用科学记数法表示应为（）

A . 2.2×10⁴ B . 22×10³ C . 2.2×10³ D . 0.22×10⁵

答案解析收藏纠错 + 选题
5. (2023九上·兰溪月考) 如图，⊙O是△ABC的外接圆，∠A＝50°，则∠BOC的度数为（　　）

A . 40° B . 50° C . 80° D . 100°

答案解析收藏纠错 + 选题
6. (2019·北京模拟) 如果a+b＝2，那么代数式 $\text{[math]}$ 的值是（　　）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
7. (2019·北京模拟) 一组数据﹣1，﹣3，2，4，0，2的众数是（　　）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
8. (2019·北京模拟) 二次函数y＝ax²+bx+c（a，b，c是常数，a＜0）的图象经过A（﹣4，﹣4），B（6，﹣4）顶点为P，则下列说法中不正确是（　　）

A . 不等式ax²+bx+c＞﹣4的解为﹣4＜x＜6 B . 关于x的方程a（x+4）（x﹣6）﹣4＝0的解与ax²+bx+c＝0的解相同 C . △PAB为等腰直角三角形，则a＝﹣ $\text{[math]}$ D . 当t≤x≤t+2时，二次函数y＝ax²+bx+c的最大值为at²+bt+c，则t≥0

答案解析收藏纠错 + 选题

二、填空题（本题共16分，每小题2分）

9. (2021·北京模拟) 如图，该正方体的主视图是形．

答案解析收藏纠错 + 选题
10. (2019·北京模拟) 若分式 $\text{[math]}$ 的值是正数，则x的取值范围是．

答案解析收藏纠错 + 选题
11. (2019·北京模拟) 一组数据2、3、﹣1、0、1的方差是．

答案解析收藏纠错 + 选题
12. (2019·北京模拟) 如图，在△ABC中，射线AD交BC于点D，BE⊥AD于E，CF⊥AD于F，请补充一个条件，使△BED≌△CFD，你补充的条件是（填出一个即可）．

答案解析收藏纠错 + 选题
13. (2019·北京模拟) 惠来县某单位组织34人分别到广州和深圳进行继续教育学习，到广州的人数是到深圳的人数的2倍多1人，求到两地的人数各是多少？设到广州的人数为x人，到深圳的人数为y人，请列出满足题意的方程组．

答案解析收藏纠错 + 选题
14. (2019·北京模拟) 如图，从一个边长为a的正方形的一角上剪去一个边长为b（a＞b）的正方形，则剩余（阴影）部分正好能够表示一个乘法公式，则这个乘法公式是（用含a，b的等式表示）．

答案解析收藏纠错 + 选题
15. (2019·北京模拟) 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点D作DE⊥AB于点E，若CD＝2，BD＝4，则AE的长是．

答案解析收藏纠错 + 选题
16. (2019·北京模拟) 直角坐标平面内，一点光源位于A（0，5）处，线段CD⊥x轴，D为垂足，C（4，1），则CD在x轴上的影长为　　，点C的影子的坐标为．

答案解析收藏纠错 + 选题

三、解答题（本题共68分，第17-21题，每小题5分，第22-27题，每小题6分，第28题7分）解答应写出文字说明、演算步骤或证明过程.

17. (2019·北京模拟) 下面是小元设计的“作已知角的角平分线”的尺规作图过程．
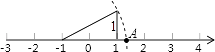
已知：如图，∠AOB．

求作：∠AOB的角平分线OP．

作法：如图，

①在射线OA上任取点C；

②作∠ACD＝∠AOB；

③以点C为圆心CO长为半径画圆，交射线CD于点P；

④作射线OP；

所以射线OP即为所求．

根据小元设计的尺规作图过程，完成以下任务．
1. （1）补全图形；
2. （2）完成下面的证明：
  证明：∵∠ACD＝∠AOB，
  
  ∴CD∥OB（）（填推理的依据）．
  
  ∴∠BOP＝∠CPO．
  
  又∵OC＝CP，
  
  ∴∠COP＝∠CPO（）（填推理的依据）．
  
  ∴∠COP＝∠BOP．
  
  ∴OP平分∠AOB．
答案解析收藏纠错 + 选题
18. (2019·北京模拟) 计算：|﹣1|﹣2sin45°+ $\text{[math]}$ ﹣2018⁰

答案解析收藏纠错 + 选题
19. (2019·北京模拟) 解不等式组 $\text{[math]}$ ，并把解表示在数轴上.

答案解析收藏纠错 + 选题
20. (2019·北京模拟) 关于x的一元二次方程x²﹣3x﹣k＝0有两个不相等的实数根．
1. （1）求k的取值范围；
2. （2）当k＝4时，求方程的根．
答案解析收藏纠错 + 选题
21. (2019·寿阳模拟) 如图，一次函数y＝x+4的图象与反比例函数y＝ $\text{[math]}$ （k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．
1. （1）求a，k的值及点B的坐标；
2. （2）若点P在x轴上，且S_△ACP＝ $\text{[math]}$ S_△BOC ，直接写出点P的坐标．
答案解析收藏纠错 + 选题
22. (2019·北京模拟) 如图，在△ABC中，AB＝AC，点D是BC边的中点，连接AD，分别过点A，C作AE∥BC，CE∥AD交于点E，连接DE，交AC于点O．
1. （1）求证：四边形ADCE是矩形；
2. （2）若AB＝10，sin∠COE＝ $\text{[math]}$ ，求CE的长．
答案解析收藏纠错 + 选题
23. (2019·北京模拟) 费尔兹奖是国际上享有崇高荣誉的一个数学奖。每4年评选一次，在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家，美籍华人丘成桐1982年获得费尔兹奖．为了让学生了解费尔兹奖得主的年龄情况，我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据，并对数据进行整理、描述和分析．下面给出了部分信息．
a．截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1（数据分成5组，各组是28≤x＜31，31≤x＜34，34≤x＜37，37≤x＜40，x≥40）：

b．如图2，在a的基础上，画出扇形统计图；

c．截止到2018年费尔兹奖得主获奖时的年龄在34≤x＜37这一组的数据是：

36

35

34

35

35

34

34

35

36

36

36

36

34

35

d．截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下：

年份

平均数

中位数

众数

截止到2018

35.58

m

37，38

根据以上信息，回答下列问题：
1. （1）依据题意，补全频数直方图；
2. （2） 31≤x＜34这组的圆心角度数多少度，并补全扇形统计图；
3. （3）统计表中中位数m的值是；
4. （4）根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征．
答案解析收藏纠错 + 选题
24. (2019·北京模拟) 如图，AB是⊙O的直径，AC切⊙O于点A，连接BC交⊙O于点D，点E是 $\text{[math]}$ 的中点，连接AE交BC于点F．
1. （1）求证：AC＝CF；
2. （2）若AB＝4，AC＝3，求∠BAE的正切值．
答案解析收藏纠错 + 选题
25. (2019·北京模拟) 如图，在Rt△ABC中，∠ABC＝90°，AB＝CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．
1. （1）求证：AE＝BF；
2. （2）连接GB，EF，求证：GB∥EF；
3. （3）若AE＝1，EB＝2，求DG的长．
答案解析收藏纠错 + 选题
26. (2019·北京模拟) 已知抛物线y＝ax²﹣4ax+4a+1（a≠0）与y轴交于点A，点A与点B关于抛物线的对称轴对称．直线l经过点B且与x轴垂直．
1. （1）求抛物线的顶点C的坐标和直线l的表达式．
2. （2）抛物线与直线l交于点P，当OP≤5时，求a的取值范围．
答案解析收藏纠错 + 选题
27. (2019·北京模拟) 在△ABC中，∠ABC＝120°，线段AC绕点A逆时针旋转60°得到线段AD，连接CD，BD交AC于P．
1. （1）若∠BAC＝α，直接写出∠BCD的度数（用含α的代数式表示）；
2. （2）求AB，BC，BD之间的数量关系；
3. （3）当α＝30°时，直接写出AC，BD的关系．
答案解析收藏纠错 + 选题
28. (2019·北京模拟) 如图，在直角△ABC中，∠C＝90°，AC＝15，BC＝20，点D为AB边上一动点，若AD的长度为m，且m的范围为0＜m＜9，在AC与BC边上分别取两点E、F，满足ED⊥AB，FE⊥ED．
1. （1）求DE的长度；（用含m的代数式表示）
2. （2）求EF的长度；（用含m的代数式表示）
3. （3）请根据m的不同取值，探索过D、E、F三点的圆与△ABC三边交点的个数．
答案解析收藏纠错 + 选题