![]()
 B .
B .  C .
C .  D .
D . 
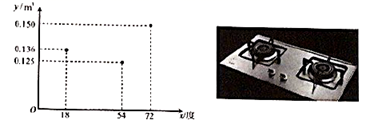
| 甲 | 乙 | 丙 | 丁 | |
| | 7 | 8 | 8 | 7 |
| s2 | 1 | 1.2 | 0.9 | 1.8 |
已知:直线 及直线
外一点P.

求作:直线 ,使
.
作法:如图,
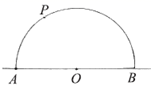
①在直线 上取一点O,以点O为圆心,
长为半径画半圆,交直线
于
两点;
②连接 ,以B为圆心,
长为半径画弧,交半圆于点Q;
③作直线 .
所以直线 就是所求作的直线.
根据小明设计的尺规作图过程:
证明:连接 ,
∵ ,
∴ .
∴ ()(填推理的依据).
∴ ()(填推理的依据).
a.甲、乙两校40名学生成绩的频数分布统计表如下:
|
成绩x 学校 |
| | | | |
| 甲 | 4 | 11 | 13 | 10 | 2 |
| 乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在 这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
| 学校 | 平均分 | 中位数 | 众数 |
| 甲 | 74.2 | n | 85 |
| 乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
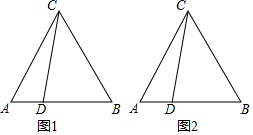
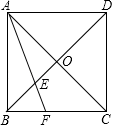
①当 时,求线段
的长;
②若 ,结合函数的图象,写出
的取值范围.

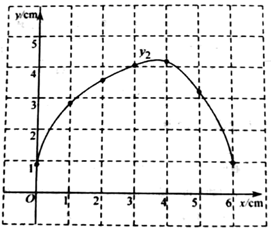
小石根据学习函数的经验,分别对函数 ,
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| | 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| | 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |