题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

初中数学中考复习综合专题：一次函数应用题

更新时间：2020-06-24 浏览次数：516 类型：一轮复习

一、综合题

1. (2020·湖州模拟) A，B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即返回.如图是它们离A城的距离y（千米）与行驶时间 x（小时）之间的函数图象.
1. （1）求甲车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；
2. （2）当它们行驶了7小时时，两车相遇，求乙车的速度及乙车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；
3. （3）当两车相距100千米时，求甲车行驶的时间.
答案解析收藏纠错 + 选题
2. (2020·温州模拟) 在抗击新冠状病毒战斗中，有152箱公共卫生防护用品要运到 $\text{[math]}$ 、 $\text{[math]}$ 两城镇，若用大小货车共15辆，则恰好能一次性运完这批防护用品，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其中用大货车运往 $\text{[math]}$ 、 $\text{[math]}$ 两城镇的运费分别为每辆800元和900元，用小货车运往 $\text{[math]}$ 、 $\text{[math]}$ 两城镇的运费分别为每辆400元和600元．
1. （1）求这15辆车中大小货车各多少辆？
2. （2）现安排其中10辆货车前往 $\text{[math]}$ 城镇，其余货车前往 $\text{[math]}$ 城镇，设前往 $\text{[math]}$ 城镇的大货车为 $\text{[math]}$ 辆，前往 $\text{[math]}$ 、 $\text{[math]}$ 两城镇总费用为 $\text{[math]}$ 元，试求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数解析式．若运往 $\text{[math]}$ 城镇的防护用品不能少于100箱，请你写出符合要求的最少费用．
答案解析收藏纠错 + 选题
3. (2020·长春模拟) 一辆轿车从甲地驶往乙地，到达乙地后返回甲地，速度是原来的1.5倍，共用t小时；一辆货车同时从甲地驶往乙地，到达乙地后停止．两车同时出发，匀速行驶．设轿车行驶的时间为x（h），两车到甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图．
1. （1）求轿车从乙地返回甲地时的速度和t的值；
2. （2）求轿车从乙地返回甲地时y与x之间的函数关系式，并写出自变量x的取值范围；
3. （3）轿车从乙地返回甲地时与货车相遇的时间．
答案解析收藏纠错 + 选题
4. (2020·珠海模拟) 某小区游泳馆夏季推出两种收费方式．方式一：先购买会员证，会员证200元，只限本人当年使用，凭证游泳每次需另付费10元：方式二：不购买会员证，每次游泳需付费20元．
1. （1）若甲计划今年夏季游泳的费用为500元，则选择哪种付费方式游泳次数比较多？
2. （2）若乙计划今年夏季游泳的次数超过15次，则选择哪种付费方式游泳花费比较少？
答案解析收藏纠错 + 选题
5. (2020·中山模拟) 某环卫公司承包了市区两个片区道路的清扫任务，需要购买某厂家A，B两种型号的马路清扫车，购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元；购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元．
1. （1）求这两种马路清扫车的单价；
2. （2）恰逢该厂举行30周年庆，决定对这两种马路清扫车开展促销活动，具体方案如下：购买A型马路清扫车按原价的八折销售，购买B型马上清扫车不超过10辆时按原价销售，超过10辆的部分按原价的七折销售．设购买x辆A种马路清扫车需要y₁元，购买x（x＞0）个B型马路清扫车需要y₂元，分别求出y₁ ， y₂关于x的函数关系式；
3. （3）若该公司承包的道路清扫面积为118000m² ，每辆A型马路清扫车每天清扫5000m² ，每辆B型马路清扫车每天清扫6000m² ，公司准备购买20辆马路清扫车，且B型马路清扫车的数量大于10．请你帮该公司设计出最省钱的购买方案．请说明理由．
答案解析收藏纠错 + 选题
6. (2023·汨罗模拟) 学校为奖励在家自主学习有突出表现的学生，决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元，4本笔记本和6支钢笔共需190元。
1. （1）分别求一本笔记本和一支钢笔的售价；
2. （2）若学校准备购进这两种奖品共90份，并且笔记本的数量不多于钢笔数量的3倍，请设计出最省钱的购买方案，并说明理由。
答案解析收藏纠错 + 选题
7. (2020·永嘉模拟) 小聪去某风景区游览，风景区内的公路如图1所示，景区内有免费的电动汽车，从古刹处出发，沿该公路开往入口（飞瀑处）（上下车时间忽略不计）．下午第一班电动汽车是13：00发车，以后每隔30分钟有一班车从古刹发车，每一班车速度均相同。小聪在景区入口飞瀑游览完后，13：00前往以下各景点游览，假设步行速度不变，离入口飞瀑处的路程s（米）与经过的时间t（分）的函数关系如图2所示。
1. （1）电动汽车的速度是米/分，小聪在草甸游览的时间是分。
2. （2）求小聪与第一班车相遇的时间t。
3. （3）小聪要在17：00前返回入口处，且在古刹游览的时间不少于45分钟，则小聪在塔林游览的最长时间是多少?
答案解析收藏纠错 + 选题
8. (2020·西安模拟) 已知A，B两地相距 $\text{[math]}$ ，甲、乙两辆货车装满货物分别从A，B两地相向而行，图中 $\text{[math]}$ 分别表示甲、乙两辆货车离A地的距离 $\text{[math]}$ 与行驶时间 $\text{[math]}$ 之间的函数关系.请你根据以上信息，解答下列问题：
1. （1）分别求出直线 $\text{[math]}$ 所对应的函数关系式；
2. （2）何时甲货车离 $\text{[math]}$ 地的距离大于乙货车离 $\text{[math]}$ 地的距离？
答案解析收藏纠错 + 选题
9. (2020·常州模拟) 某景区的三个景点 $\text{[math]}$ 在同一线路上，甲、乙两名游客从景点A出发，甲步行到景点C乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间 $\text{[math]}$ (分钟)的函数图象如图所示.根据以上信息回答下列问题：
1. （1）乙出发后多长时间与甲相遇?
2. （2）若当甲到达景点C时，乙与景点C的路程为 $\text{[math]}$ 米，则乙从景点B步行到景点C的速度是多少?
答案解析收藏纠错 + 选题
10. (2020·绍兴模拟) 某商店准备购进A, B两种商品，A种商品每件的进价比B种商品每件的进价多20
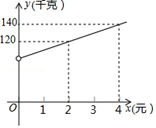
元，用3000元购进A种商品和用1800元购进B种商品的数量相同.商店将A种商品

每件的售价定为80元，B种商品每件的售价定为45元.
1. （1） A种商品每件的进价和B种商品每件的进价各是多少元?
2. （2）商店计划用不超过1560元的资金购进 $\text{[math]}$ 两种商品共40件，其中A种商品的数量不低于B种商品数量的一半，该商店有几种进货方案？
3. （3）端午节期间，商店开展优惠促销活动，决定对每件A种商品售价优惠M（ $\text{[math]}$ ）元，B种商品售价不变，在（2）条件下，请设计出销售这40件商品获得总利润最大的进货方案.
答案解析收藏纠错 + 选题
11. (2020·宽城模拟) 李师傅驾车从甲地去乙地，途中在加油站加了一次油，加油时，车载电脑显示油箱中剩余油量为4升。已知汽车行驶时每小时的耗油量一定，设油箱中剩余油量为y（升），汽车行驶时间为x（时），y与x之间的函数图象如图所示。
1. （1）求李师傅加油前y与x之间的函数关系式。
2. （2）求a的值。
3. （3）求李师傅在加油站的加油量。
答案解析收藏纠错 + 选题
12. (2020·长春模拟) 星期天，小强骑自行车到效外与同学一起游玩。从家出发2小时到达目的地，游玩3小时后按原路以原速返回，小强离家4小时40分钟后，妈妈驾车沿相同路线迎接小强，如图是他们离家的路程y（千米）与时间x（时）的函数图象。已知小强骑车的速度为15千米/时，妈妈驾车的速度为60千米/时。
1. （1）小强家与游玩地的距离是多少？
2. （2）妈妈出发多长时间与小强相遇？
答案解析收藏纠错 + 选题
13. (2020七下·蒙阴月考) 在绿化某县城与高速公路的连接路段中，需购买罗汉松、雪松两种树苗共400株，罗汉松树苗每株60元，雪松树苗每株70元．相关资料表明：罗汉松、雪松树苗的成活率分别为70%，90%．
1. （1）若购买这两种树苗共用去26500元，则罗汉松、雪松树苗各购买多少株?
2. （2）绿化工程来年一般都要将死树补上新苗，现要使该两种树苗来年共补苗不多于80株，则罗汉松树苗至多购买多少株?
3. （3）在（2）的条件下，应如何选购树苗，才能使购买树苗的费用最低?请求出最低费用．
答案解析收藏纠错 + 选题

14. (2020·温州模拟) 温州某一企业原先一次性口罩和防雾霾口罩生产信息如下表：

口罩类型	材料成本(不含人工)	出厂价	产量(一人一天)
一次性口罩	0.1元/个	0.2元/个	2000个
防雾霾口罩	2.5元/个	4元/个	200个

已知该企业有12名工人，工资每人每天150元。该企业原来每天产量共15000个口罩。

（1）求原先企业安排生产一次性口罩和防雾霾口罩各有多少人。
（2）经一段时间运行，企业发现每天销售的防雾霾口罩，最多只能卖900个。而一次性口罩可以全部销售，市场缺口较大。怎么安排生产口罩的人数可以使该企业每一天获得利润最大。最大利润是多少？(注：没有销售的口罩，作为库存暂时当做不赚不亏)。

（3）在疫情期间，为了配合政府防疫工作，该厂改为全部生产一次性口罩。因为原材料价格暴涨，口罩的材料成本和出厂价分别变为0.6元/个和1元/个。一部分员工因为滞留在外，无法及时回来工作。所以该厂提高了剩余老员工的工资，也招募了几个新员工过来且老员工人数多于新员工。信息如下表：

员工类型	每日工资	一次性口罩产量(一人一天)
老员工	300元/天	2000个
新员工	200元/天	1000个

要是该厂的利润达到4000元/天。求该厂留下来的老员工和招募的新员工人数。

答案解析收藏纠错 + 选题

15. (2020·慈溪模拟) 某快递公司有甲、乙两辆货车沿同一路线从A地到B地配送货物。某天两车同时从A地出发，驶向B地，途中乙车由于出现故障，停车修理了一段时间，修理完毕后，乙车加快了速度匀速驶向B地；甲车从A地到B地速度始终保持不变．如图所示是甲、乙两车之间的距离y(km)与两车出发时间x(h)的函数图象．根据相关信息解答下列问题：
1. （1）点Ｍ的坐标表示的实际意义是什么？
2. （2）求出MN所表示的关系式，并写出乙故障后的速度。
3. （3）求故障前两车的速度以及a的值。
答案解析收藏纠错 + 选题
16. (2020·绍兴模拟) 小明星期天上午8：00从家出发到离家36千米的书城买书，他先从家出发骑公共自行车到公交车站，等了12分钟的车，然后乘公交车于9：48分到达书城(假设在整个过程中小明骑车的速度不变，公交车匀速行驶，小明家、公交车站、书城依次在一条笔直的公路旁)。如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象，其中线段AB对应的函数表达式为y=kx+6。
1. （1）求小明骑公共自行车的速度；
2. （2）求线段CD对应的函数表达式：
3. （3）求出发时间x在什么范围时，小明离公交车站的路程不超过3千米？
答案解析收藏纠错 + 选题
17. (2021·沙依巴克模拟) 为迎接“五一”国际劳动节，某商场计划购进甲、乙两种品牌的 $\text{[math]}$ 恤衫共100件，已知乙品牌每件的进价比甲品牌每件的进价贵30元，且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.
1. （1）求甲、乙两种品牌每件的进价分别是多少元？
2. （2）商场决定甲品牌以每件50元出售，乙品牌以每件100元出售.为满足市场需求，购进甲种品牌的数量不少于乙种品牌数量的4倍，请你确定获利最大的进货方案，并求出最大利润.
答案解析收藏纠错 + 选题

18. (2020·平阳模拟) 下表是小丽在某路口统计20分钟各种车辆通过情况的记录表，其中空格处的字迹已模糊。

	电瓶车	公交车	货车	小轿车	合计(车流总量)
(第一时段)8：50~9：00		m		86	161
(第二时段)9：00~9：10	7n	m	n	99
合计			30	185

（1）根据表格信息，在表格中填写第一时段电瓶车和货车的数量。
（2）在第二时段内，电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半，且两个时段的电瓶车总数为170辆。
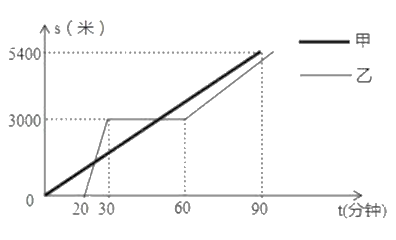
①求m，n的值。

②因为第二时段内车流总量较多，造成了交通拥堵现象，据估计，该时段内，每增加1辆公交车，可减少8辆小轿车和5辆电瓶年，若要使得第二时段和第一时段的车流总量最接近，则应增加几辆公交车？

答案解析收藏纠错 + 选题

19. (2020·长兴模拟) 为了组织一个50人的旅游团开展“乡间民俗”游，旅游团住村民家，住宿客房有三人间、二人间、单人间三种，收费标准是三人间每人每晚20元，二人间每人每晚30元，单人间每人每晚50元，旅游团共住20间客房。
1. （1）若单人间住了4间，且恰好将20间客房住满，求三人间和二人间各入住多少间？
2. （2）设旅游团预定的房间中单人间有x间，所需总的住宿费为W，求W关于x的函数关系式；
3. （3）旅游团如何，安排住宿才能够使得住宿费最低？最低费用为多少？
答案解析收藏纠错 + 选题
20. (2020·陕西模拟) 我国很多城市水资源缺乏，为了加强居民的节水意识，某市制定了每月用水8吨以内(包括8吨)和用水8吨以上两种收费标准(收费标准：每吨水的价格)，某用户每月应交水费y(元)是用水量x(吨)的函数，其函数图象如图所示。
1. （1）求出自来水公司在这两个用水范围内的收费标准；
2. （2）若芳芳家6月份共交水费28.1元，请写出用水量超过8吨时应交水费y(元)与用水量x(吨)之间的函数关系，并求出芳芳家6月份的用水量。
答案解析收藏纠错 + 选题
21. (2022八下·鲅鱼圈期末) 为更新树木品种，某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵，其中甲种树苗的单价为6元/棵，购买乙种树苗所需费用y（元）与购买数量x（棵）之间的函数关系如图所示.
1. （1）求出y与x的函数关系式；
2. （2）若在购买计划中，乙种树苗的数量不超过35棵，但不少于甲种树苗的数量.请设计购买方案，使总费用最低，并求出最低费用.
答案解析收藏纠错 + 选题
22. (2020九下·江阴期中) 如图①，点A表示小明家，点B表示学校.小明妈妈骑车带着小明去学校，到达C处时发现数学书没带，于是妈妈立即骑车原路回家拿书后再追赶小明，同时小明步行去学校，到达学校后等待妈妈.假设拿书时间忽略不计，小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y₁米，小明离C处的距离为y₂米，如图②，折线O-D-E-F表示y₁与x的函数图象；折线O-G-F表示y₂与x的函数图象.
1. （1）小明的速度为m/min，图②中a的值为.
2. （2）设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时，求出y与x的函数表达式.
答案解析收藏纠错 + 选题
23. (2020·台州模拟) 自2017年3月起，成都市中心城区居民用水实行以户为单位的三级阶梯收费办法：
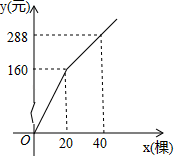
第I级：居民每户每月用水18吨以内含18吨每吨收水费a元；

第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过部分每吨收水费b元；

第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第I、Ⅱ级标准收费，超过部分每吨收水费c元.

设一户居民月用水x吨，应缴水费为y元，y与x之间的函数关系如图所示
1. （1）根据图象直接作答：a＝，b＝；
2. （2）求当x≥25时y与x之间的函数关系；
3. （3）把上述水费阶梯收费办法称为方案①，假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费，请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.（写出过程）
答案解析收藏纠错 + 选题
24. (2020·官渡模拟) 在创建全国文明城市过程中，官渡区决定购买A、B两种树苗对某路段道路进行绿化改造.已知购买A种树苗5棵，B种树苗3棵，需要840元；购买A种树苗3棵，B种树苗5棵，需要760元.
1. （1）求购买A、B两种树苗每棵各需多少元?
2. （2）现需购进这两种树苗共100棵，考虑到绿化效果和资金周转，购进A种树苗不能少于30棵，且用于购买这两种树苗的资金不能超过10000元，怎样购买所需资金最少?
答案解析收藏纠错 + 选题
25. (2020·滨海模拟) 某商店销售1台A型和3台B型电脑的利润为550元，销售2台A型和3台B型电脑的利润为650元．
1. （1）求每台A型电脑和B型电脑的销售利润；
2. （2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
  ①求y与x的关系式；
  
  ②该商店购进A型、B型各多少台，才能使销售利润最大？
答案解析收藏纠错 + 选题
26. (2020九下·东台期中) 为增强学生体质，某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中，小明和小亮同时起跑，同时到达终点；所跑的路程S（米）与所用的时间t（秒）之间的函数图象如图所示：
1. （1）当80≤t≤180时，求小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式；
2. （2）求他们第一次相遇的时间是起跑后的第几秒？
答案解析收藏纠错 + 选题
27. (2020·石家庄模拟) 有一科技小组进行了机器人行走性能试验．在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，历时7min同时到达C点，甲机器人前3分钟以am/min的速度行走，乙机器人始终以60m/min的速度行走，如图是甲、乙两机器人之间的距离y（m）与他们的行走时间x（min）之间的函数图象，请结合图象，回答下列问题：
1. （1） A、B两点之间的距离是m ， A、C两点之间的距离是m ， a＝m/min：
2. （2）求线段EF所在直线的函数表达式？
3. （3）设线段FG∥x轴．
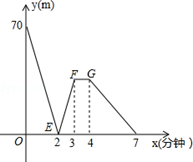
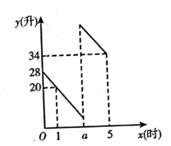
  ①当3≤x≤4时，甲机器人的速度为m/min ．
答案解析收藏纠错 + 选题
28. (2020八下·江都期中) 某电脑公司经销甲种型号电脑，今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑，去年的销售额为10万元，那么今年的销售额只有8万元.
1. （1）今年三月份甲种型号电脑每台的售价为多少元?
2. （2）为增加收入，电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元，乙种型号电脑每台的进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台，则有几种进货方案?
3. （3）如果乙种型号电脑每台的售价为3800元，为打开乙种型号电脑的销路，公司决定每售出一台乙种型号电脑，返还顾客现金a元，要使(2)中所有方案的获利相同，那么a的值应是多少？
答案解析收藏纠错 + 选题
29. (2020·凉山模拟) 某校九年级决定购买学习用具对在本次适应性考以中成绩突出的同学进行奖励，其中计划购买，A、B两种型号的钢笔共45支，已知A种钢笔的单价为7元/支，购买B种钢笔所需费用y(元)与购买数量x(支)之间存在如图所示的函数关系式．
1. （1）求y与x的函数关系式；
2. （2）若购买计划中，B种钢笔的数最不超过35支，但不少于A种钢笔的数量，请设计购买方案，使总费用最低，并求出最低费用．
答案解析收藏纠错 + 选题
30. (2019九上·双台子月考) 铁岭市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y(千克)与每千克降价x(元)(0＜x＜20)之间满足一次函数关系，其图象如图所示：
1. （1）求y与x之间的函数关系式；
2. （2）商贸公司要想获利2090元，则这种干果每千克应降价多少元？
3. （3）该干果每千克降价多少元时，商贸公司获利最大？最大利润是多少元？
答案解析收藏纠错 + 选题

试卷信息