 B .
B . 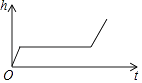 C .
C . 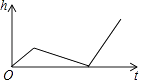 D .
D . 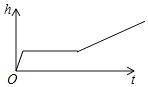


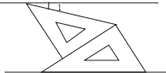
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是.

|
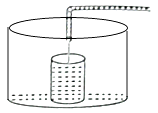
观察时刻 |
8:00 |
8:06 |
8:18 |
(注:“青岛80km”表示离青岛的距离为80km) |
|
路牌内容 |
青岛80km |
青岛70km |
青岛50km |
从8点开始,记汽车行驶的时间为t(min),汽车离青岛的距离为s(km),则s与t的关系式为.


①
②


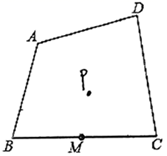
证明:∵ ,
(已知)
∴ ()
∴ ()
∴ ()
又∵ (已知)
∴ ()
∴ ()
∴ .

材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘a•a…,a记为an , 如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴am•an=am+n=M•N,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga (a>0且a≠1,M>0,N>0)