江苏省徐州市2020年数学中考模拟试卷(5月A卷）

更新时间：2024-11-06 浏览次数：158 类型：中考模拟

一、选择题

1. (2022·道外模拟) 5的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·徐州模拟) 计算﹣3a•（2b），正确的结果是（）

A . ﹣6ab B . 6ab C . ﹣ab D . ab

答案解析收藏纠错 + 选题
3. (2020·河北模拟) 如图是一个由5个相同的正方体组成的几何体，它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·徐州模拟) 如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的周长是6，则△ABC的周长是（）

A . 24 B . 14 C . 12 D . 6

答案解析收藏纠错 + 选题
5. (2021·孟津模拟) 生物学家发现了一种病毒，其长度约为 $\text{[math]}$ ，将数据0. 00000032用科学记数法表示正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·徐州模拟) 某兴趣小组为了解我市气温变化情况，记录了今年1月份连续6天的最低气温（单位：℃）： $\text{[math]}$ ，关于这组数据，下列结论不正确的是（）

A . 平均数是-2 B . 中位数是-2 C . 众数是-2 D . 方差是7

答案解析收藏纠错 + 选题
7. (2020·徐州模拟) 一元二次方程 $\text{[math]}$ 的根的情况为（）

A . 没有实数根 B . 只有一个实数根 C . 两个相等的实数根 D . 两个不相等的实数根

答案解析收藏纠错 + 选题
8. (2019八下·勃利期末) 如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作Rt△ABC，使∠BAC=90°，∠ACB=30°，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2020·徐州模拟) 使分式 $\text{[math]}$ 有意义的x的取值范围为.

答案解析收藏纠错 + 选题
10. (2024九上·阳山期中) 一元二次方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
11. (2021七下·阜南期末) 分解因式3a²-3b²=．

答案解析收藏纠错 + 选题
12. (2020七上·农安期末) 已知2a﹣3b=7，则8+6b﹣4a=．

答案解析收藏纠错 + 选题
13. (2024九上·光明开学考) 若正多边形的一个外角是40°，则这个正多边形的边数是.

答案解析收藏纠错 + 选题
14. (2022九下·定陶期中) 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形.若圆锥的母线长l为6cm，扇形的圆心角θ＝120°，则该圆锥的侧面积为cm².（结果保留π）

答案解析收藏纠错 + 选题
15. (2024九下·绵阳月考) 从﹣1，2，3，﹣6这四个数中任选两数，分别记作m，n，那么点（m，n）在函数y= $\text{[math]}$ 图象上的概率是．

答案解析收藏纠错 + 选题
16. (2020·徐州模拟) 已知点A是直线y=x+1上一点，其横坐标为﹣ $\text{[math]}$ ，若点B与点A关于y轴对称，则点B的坐标为．

答案解析收藏纠错 + 选题
17. (2020·徐州模拟) 如图，将▱ABCD沿EF对折，使点A落在点C处，若∠A＝60°，AD＝4，AB＝8，则AE的长为.

答案解析收藏纠错 + 选题
18. (2022九下·武汉月考) 已知抛物线y=x²+2x﹣3与x轴交于A，B两点（点A在点B的左侧），将这条抛物线向右平移m（m＞0）个单位长度，平移后的抛物线与x轴交于C，D两点（点C在点D的左侧），若B，C是线段AD的三等分点，则m的值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020·徐州模拟) 计算：
1. （1）（﹣2017）⁰﹣（ $\text{[math]}$ ）^﹣¹+ $\text{[math]}$ ；
2. （2）化简：（ $\text{[math]}$ ﹣a）÷ $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2020·徐州模拟)
1. （1）解方程： $\text{[math]}$ ＝1﹣ $\text{[math]}$ ；
2. （2）解不等式组： $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2020·徐州模拟) 端午节当天，小明带了四个粽子（除味道不同外，其它均相同），其中两个是大枣味的，另外两个是火腿味的，准备按数量平均分给小红和小刚两个好朋友．
1. （1）请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性．
2. （2）请你计算小红拿到的两个粽子刚好是同一味道的概率．
答案解析收藏纠错 + 选题
22. (2020·徐州模拟) 在“宏扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如下：
1. （1）如图，希望参加活动C占20%，希望参加活动B占15%，则被调查的总人数为 ▲ 人，扇形统计图中，希望参加活动D所占圆心角为 ▲ 度，根据题中信息补全条形统计图.
2. （2）学校现有800名学生，请根据图中信息，估算全校学生希望参加活动A有多少人？
答案解析收藏纠错 + 选题
23. (2021九上·六盘水月考) 如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．
1. （1）求证：四边形ABCD是菱形；
2. （2）若∠ADB=30°，BD=6，求AD的长．
答案解析收藏纠错 + 选题
24. (2020九上·海珠期中) 如图，△ABC内接于⊙O，∠B=60⁰ ， CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．
1. （1）求证：PA是⊙O的切线；
2. （2）若PD= $\text{[math]}$ ，求⊙O的直径．
答案解析收藏纠错 + 选题
25. (2020九上·乌拉特前旗期中)
如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？

答案解析收藏纠错 + 选题
26. (2020·徐州模拟) 如图，一艘船以每小时30海里的速度向北偏东75°方向航行，在点 $\text{[math]}$ 处测得码头 $\text{[math]}$ 的船的东北方向，航行40分钟后到达 $\text{[math]}$ 处，这时码头 $\text{[math]}$ 恰好在船的正北方向，在船不改变航向的情况下，求出船在航行过程中与码头 $\text{[math]}$ 的最近距离.（结果精确的0.1海里，参考数据 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
27. (2020·徐州模拟) 如图1和图2，在△ABC中，AB＝13，BC＝14， $\text{[math]}$ .
1. （1）探究：如图1，AH⊥BC于点H，则AH＝，AC＝，△ABC的面积 $\text{[math]}$ ＝.
2. （2）拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $\text{[math]}$ ＝0）.
  ①用含x、m或n的代数式表示 $\text{[math]}$ 及 $\text{[math]}$ ；
  
  ②求(m+n)与x的函数关系式，并求(m+n)的最大值和最小值；
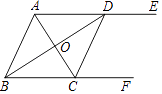
3. （3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
  发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.
答案解析收藏纠错 + 选题
28. (2022·济宁模拟) 如图，抛物线y=﹣x²+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C
1. （1）求抛物线的解析式；
2. （2）点P从点A出发，以每秒 $\text{[math]}$ 个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x=3上．
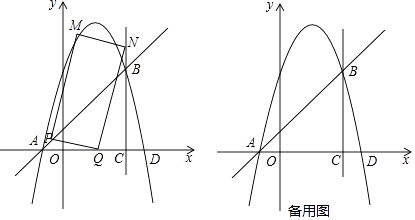
  ①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
  ②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．
答案解析收藏纠错 + 选题