2020年江苏省中考数学分类汇编专题11 图形的变换与视图

更新时间：2020-09-10 浏览次数：248 类型：二轮复习

一、单选题

1. (2023八下·东明期中) 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020九上·兰山期末) 下列图形中，属于中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·游仙模拟) “致中和，天地位焉，万物育焉.”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光.在下列与扬州有关的标识或简图中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020九上·昆都仑期末) 如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体，这个几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023·南岳模拟) 如图，一个几何体由5个相同的小正方体搭成，该几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2020·连云港) 下图是由4个大小相同的正方体搭成的几何体，这个几何体的主视图是（）.

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022·柳江模拟) 如图是由4个小正方体组合成的几何体，该几何体的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2021·阳新模拟) 如图是某几何体的三视图，该几何体是（）

A . 圆柱 B . 三棱柱 C . 四棱柱 D . 四棱锥

答案解析收藏纠错 + 选题
9. (2023九上·兰溪月考) 以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
10. (2024八下·榕城月考) 下列图形中，是轴对称图形但不是中心对称图形的是（）

A . 圆 B . 等腰三角形 C . 平行四边形 D . 菱形

答案解析收藏纠错 + 选题
11. (2024九上·青阳期末) 在平面直角坐标系中，点 $\text{[math]}$ 关于原点对称的点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2020·镇江) 如图①，AB＝5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，点P，Q分别在射线AM、BN上，PQ∥AB.设AP＝x，QD＝y.若y关于x的函数图象（如图②）经过点E(9，2)，则cosB的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2023九上·江岸月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A按逆时针方向旋转得到 $\text{[math]}$ .若点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023·游仙模拟) 如图，等边 $\text{[math]}$ 的边长为3，点D在边 $\text{[math]}$ 上， $\text{[math]}$ ，线段 $\text{[math]}$ 在边 $\text{[math]}$ 上运动， $\text{[math]}$ ，有下列结论：

① $\text{[math]}$ 与 $\text{[math]}$ 可能相等；② $\text{[math]}$ 与 $\text{[math]}$ 可能相似；③四边形 $\text{[math]}$ 面积的最大值为 $\text{[math]}$ ；④四边形 $\text{[math]}$ 周长的最小值为 $\text{[math]}$ .其中，正确结论的序号为（）

A . ①④ B . ②④ C . ①③ D . ②③

答案解析收藏纠错 + 选题

二、填空题

15. (2020九上·丰台期中) 点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）.这个图案绕点O至少旋转°后能与原来的图案互相重合.

答案解析收藏纠错 + 选题
16. (2020·镇江) 如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A₁B₁C₁ ，点P、Q分别是AB、A₁C₁的中点，PQ的最小值等于.

答案解析收藏纠错 + 选题
17. (2021·滕州模拟) 如图，在正方形网格中，每个小正方形的边长均为1，△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C₁ ， △DEF的周长为C₂ ，则 $\text{[math]}$ 的值等于.

答案解析收藏纠错 + 选题
18. (2020九上·丹东月考) 如图， $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
19. (2020·盐城) 如图，已知点 $\text{[math]}$ ，直线 $\text{[math]}$ 轴，垂足为点 $\text{[math]}$ 其中 $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 关于直线l对称，且 $\text{[math]}$ 有两个顶点在函数 $\text{[math]}$ 的图像上，则k的值为：.

答案解析收藏纠错 + 选题
20. (2020·无锡) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 连接 $\text{[math]}$ ， $\text{[math]}$ ，相交于点O，则 $\text{[math]}$ 面积最大值为.

答案解析收藏纠错 + 选题
21. (2020·苏州) 如图，在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ，垂足为D， $\text{[math]}$ .若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
22. (2022·福田模拟) 如图，在平面直角坐标系中，点A、B的坐标分别为 $\text{[math]}$ 、 $\text{[math]}$ ，点 $\text{[math]}$ 在第一象限内，连接 $\text{[math]}$ 、 $\text{[math]}$ .已知 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

23. (2020·泰州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的动点（与 $\text{[math]}$ 、 $\text{[math]}$ 不重合）， $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ .
1. （1）用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ 的长；
2. （2）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数表达式，并求当 $\text{[math]}$ 随 $\text{[math]}$ 增大而减小时 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
24. (2021九上·德保期中) 如图，在矩形 $\text{[math]}$ 中，E是 $\text{[math]}$ 的中点， $\text{[math]}$ ，垂足为F.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
25. (2020·南京) 如图①，要在一条笔直的路边l上建一个燃气站，向l同侧的A、B两个城镇分别发铺设管道输送燃气，试确定燃气站的位置，使铺设管道的路线最短.
1. （1）如图②，作出点A关于l的对称点 $\text{[math]}$ ，线 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点C的位置即为所求，即在点C处建气站，所得路线ACB是最短的，为了让明点C的位置即为所求，不妨在l直线上另外任取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，证明 $\text{[math]}$ ，请完成这个证明.
2. （2）如果在A、B两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案（不需说明理由），
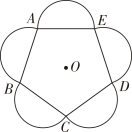
  ①生市保护区是正方形区城，位置如图③所示
  
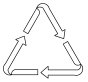
  ②生态保护区是圆形区域，位置如图④所示.
答案解析收藏纠错 + 选题
26. (2020·南京) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中，D、 $\text{[math]}$ 分别是AB、 $\text{[math]}$ 上一点， $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求证： $\text{[math]}$ 证明的途径可以用如框图表示，请填写其中的空格 $\text{[math]}$
2. （2）当 $\text{[math]}$ 时，判断 $\text{[math]}$ 与 $\text{[math]}$ 是否相似，并说明理由
答案解析收藏纠错 + 选题
27. (2020·宿迁) 如图
1. （1）（感知）如图①，在四边形ABCD中，∠C=∠D=90°，点E在边CD上，∠AEB=90°，求证： $\text{[math]}$ = $\text{[math]}$ .
2. （2）（探究）如图②，在四边形ABCD中，∠C=∠ADC=90°，点E在边CD上，点F在边AD的延长线上，∠FEG=∠AEB=90°，且 $\text{[math]}$ = $\text{[math]}$ ，连接BG交CD于点H.求证：BH=GH.
3. （3）（拓展）如图③，点E在四边形ABCD内，∠AEB+∠DEC=180°，且 $\text{[math]}$ = $\text{[math]}$ ，过E作EF交AD于点F，若∠EFA=∠AEB，延长FE交BC于点G.求证：BG=CG.
答案解析收藏纠错 + 选题
28. (2020·南通) （了解概念）
有一组对角互余的凸四边形称为对余四边形，连接这两个角的顶点的线段称为对余线.
1. （1）（理解运用）
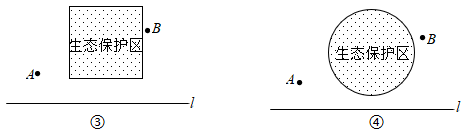
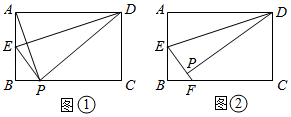
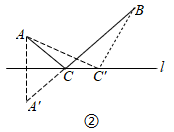
  如图①，对余四边形ABCD中，AB＝5，BC＝6，CD＝4，连接AC.若AC＝AB，求sin∠CAD的值；
2. （2）如图②，凸四边形ABCD中，AD＝BD，AD⊥BD，当2CD²+CB²＝CA²时，判断四边形ABCD是否为对余四边形.证明你的结论；
3. （3）（拓展提升）
  在平面直角坐标系中，点A（﹣1，0），B（3，0），C（1，2），四边形ABCD是对余四边形，点E在对余线BD上，且位于△ABC内部，∠AEC＝90°+∠ABC.设 $\text{[math]}$ ＝u，点D的纵坐标为t，请直接写出u关于t的函数解析式.
答案解析收藏纠错 + 选题
29. (2021九上·包头月考) 矩形ABCD中，AB＝8，AD＝12.将矩形折叠，使点A落在点P处，折痕为DE.
1. （1）如图①，若点P恰好在边BC上，连接AP，求 $\text{[math]}$ 的值；
2. （2）如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长.
答案解析收藏纠错 + 选题
30. (2020·淮安)
1. （1）（初步尝试）
  如图①，在三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 折叠，使点B与点C重合，折痕为 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为；
2. （2）（思考说理）
  如图②，在三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 折叠，使点B与点C重合，折痕为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
3. （3）如图③，在三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿过顶点 $\text{[math]}$ 的直线折叠，使点B落在边 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕为 $\text{[math]}$ .
  ①求线段 $\text{[math]}$ 的长；
  
  ②若点O是边 $\text{[math]}$ 的中点，点P为线段 $\text{[math]}$ 上的一个动点，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠得到 $\text{[math]}$ ，点A的对应点为点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点F，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题