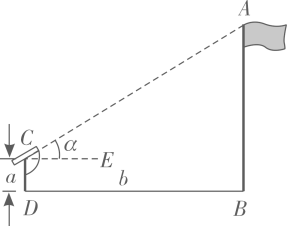
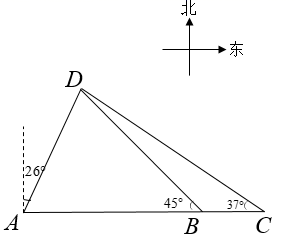
Ⅰ.在 中,
,在探究三边关系时,通过画图,度量和计算,收集到,组数据如下表:(单位:厘米)
| | 2.8 | 2.7 | 2.6 | 2.3 | 2 | 1.5 | 0.4 |
| | 0.4 | 0.8 | 1.2 | 1.6 | 2 | 2.4 | 2.8 |
| | 3.2 | 3.5 | 3.8 | 3.9 | 4 | 3.9 | 3.2 |
Ⅱ.根据学习函数的经验,选取上表中 和
的数据进行分析;
设
,以
为坐标,在图
所示的坐标系中描出对应的点;
连线;
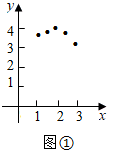
Ⅲ.观察思考
结合表中的数据以及所面的图像,猜想.当 ▲ 时,y最大;
Ⅳ.进一步C猜想:若 中,
,斜边
为常数,
),则
▲ 时,
最大.
推理证明
Ⅴ.对(4)中的猜想进行证明.


