2016年高考理数真题试卷（全国丙卷）

更新时间：2016-06-17 浏览次数：782 类型：高考真卷

一、选择题:本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2016·新课标Ⅲ卷理) 设集合S={x|（x﹣2）（x﹣3）≥0}，T={x|x＞0}，则S∩T=（　　）

A . [2，3] B . （﹣∞，2]∪[3，+∞） C . [3，+∞） D . （0，2]∪[3，+∞）

答案解析收藏纠错 + 选题
2. (2016·新课标Ⅲ卷理) 若z=1+2i，则 $\text{[math]}$ =（　　）

A . 1 B . ﹣1 C . i D . ﹣i

答案解析收藏纠错 + 选题
3. (2016·新课标Ⅲ卷理) 已知向量 $\text{[math]}$ =（ $\text{[math]}$ ， $\text{[math]}$ ）， $\text{[math]}$ =（ $\text{[math]}$ ， $\text{[math]}$ ），则∠ABC=（　　）

A . 30° B . 45° C . 60° D . 120°

答案解析收藏纠错 + 选题
4. (2020高一下·永寿月考)
某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图，图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃，下面叙述不正确的是（　　）

A . 各月的平均最低气温都在0℃以上 B . 七月的平均温差比一月的平均温差大 C . 三月和十一月的平均最高气温基本相同 D . 平均最高气温高于20℃的月份有5个

答案解析收藏纠错 + 选题
5. (2021高三上·哈尔滨月考) 若tanα= $\text{[math]}$ ，则cos²α+2sin2α=（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022高一上·齐齐哈尔期中) 已知a= $\text{[math]}$ ，b= $\text{[math]}$ ，c= $\text{[math]}$ ，则（　　）

A . b＜a＜c B . a＜b＜c C . b＜c＜a D . c＜a＜b

答案解析收藏纠错 + 选题
7. (2016·新课标Ⅲ卷理)
执行如图程序框图，如果输入的a=4，b=6，那么输出的n=（　　）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
8. (2016·新课标Ⅲ卷理) 在△ABC中，B= $\text{[math]}$ ，BC边上的高等于 $\text{[math]}$ BC，则cosA=（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020高二上·静乐月考)
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（　　）

A . 18+36 $\text{[math]}$ B . 54+18 $\text{[math]}$ C . 90 D . 81

答案解析收藏纠错 + 选题
10. (2016·新课标Ⅲ卷理) 在封闭的直三棱柱ABC﹣A₁B₁C₁内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA₁=3，则V的最大值是（　　）

A . 4π B . $\text{[math]}$ C . 6π D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2016·新课标Ⅲ卷理) 已知O为坐标原点，F是椭圆C： $\text{[math]}$ =1（a＞b＞0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2016·新课标Ⅲ卷理) 定义“规范01数列”{a_n}如下：{a_n}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a₁ ， a₂ ， …，a_k中0的个数不少于1的个数，若m=4，则不同的“规范01数列”共有（　　）

A . 18个 B . 16个 C . 14个 D . 12个

答案解析收藏纠错 + 选题

二、填空题：本大题共4小题，每小题5分.

13. (2021高二上·雅安期末) 若x，y满足约束条件 $\text{[math]}$ ，则z=x+y的最大值为．

答案解析收藏纠错 + 选题
14. (2016·新课标Ⅲ卷理) 函数y=sinx﹣ $\text{[math]}$ cosx的图象可由函数y=sinx+ $\text{[math]}$ cosx的图象至少向右平移个单位长度得到．

答案解析收藏纠错 + 选题
15. (2016·新课标Ⅲ卷理) 已知f（x）为偶函数，当x＜0时，f（x）=ln（﹣x）+3x，则曲线y=f（x）在点（1，﹣3）处的切线方程是．

答案解析收藏纠错 + 选题
16. (2016·新课标Ⅲ卷理) 已知直线l：mx+y+3m﹣ $\text{[math]}$ =0与圆x²+y²=12交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，若|AB|=2 $\text{[math]}$ ，则|CD|=．

答案解析收藏纠错 + 选题

三、解答题：解答应写出文字说明，证明过程或演算步骤.

17. (2022·无锡模拟) 已知数列{a_n}的前n项和S_n=1+λa_n ，其中λ≠0．
1. （1）证明{a_n}是等比数列，并求其通项公式；
2. （2）若S₅= $\text{[math]}$ ，求λ．
答案解析收藏纠错 + 选题
18. (2016·新课标Ⅲ卷理)
如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
注：年份代码1﹣7分别对应年份2008﹣2014．
1. （1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；
2. （2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
  附注：
  参考数据： $\text{[math]}$ =9.32， $\text{[math]}$ =40.17， $\text{[math]}$ =0.55， $\text{[math]}$ ≈2.646．
  参考公式： $\text{[math]}$ ，
  回归方程 $\text{[math]}$ 中斜率和截距的最小二乘估计公式分别为：
  $\text{[math]}$ ， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2016·新课标Ⅲ卷理)
如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．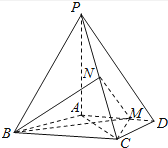
1. （1）证明：MN∥平面PAB；
2. （2）求直线AN与平面PMN所成角的正弦值．
答案解析收藏纠错 + 选题
20. (2016·新课标Ⅲ卷理) 已知抛物线C：y²=2x的焦点为F，平行于x轴的两条直线l₁ ， l₂分别交C于A，B两点，交C的准线于P，Q两点．
1. （1）若F在线段AB上，R是PQ的中点，证明AR∥FQ；
2. （2）若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程．
答案解析收藏纠错 + 选题
21. (2016·新课标Ⅲ卷理) 设函数f（x）=acos2x+（a﹣1）（cosx+1），其中a＞0，记f（x）的最大值为A．
1. （1）求f′（x）；
2. （2）求A；
3. （3）证明：|f′（x）|≤2A．
答案解析收藏纠错 + 选题
22. (2016·新课标Ⅲ卷理)
[选修4-1：几何证明选讲]如图，⊙O中弧AB 的中点为P，弦PC，PD分别交AB于E，F两点．
1. （1）若∠PFB=2∠PCD，求∠PCD的大小；
2. （2）若EC的垂直平分线与FD的垂直平分线交于点G，证明：OG⊥CD．
答案解析收藏纠错 + 选题
23. (2016·新课标Ⅲ卷理) [选修4-4：坐标系与参数方程]
在直角坐标系xOy中，曲线C₁的参数方程为 $\text{[math]}$ （α为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C₂的极坐标方程为ρsin（θ+ $\text{[math]}$ ）=2 $\text{[math]}$ ．
1. （1）写出C₁的普通方程和C₂的直角坐标方程；
2. （2）设点P在C₁上，点Q在C₂上，求|PQ|的最小值及此时P的直角坐标．
答案解析收藏纠错 + 选题
24. (2016·新课标Ⅲ卷理) [选修4-5：不等式选讲]
已知函数f（x）=|2x﹣a|+a．
1. （1）当a=2时，求不等式f（x）≤6的解集；
2. （2）设函数g（x）=|2x﹣1|，当x∈R时，f（x）+g（x）≥3，求a的取值范围．
答案解析收藏纠错 + 选题