 B .
B .  C .
C .  D .
D . 


 D .
D . 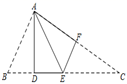

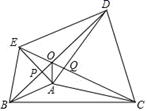




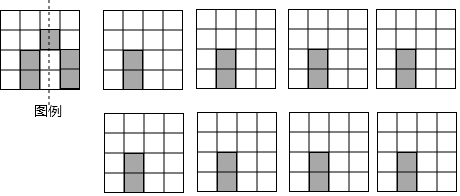
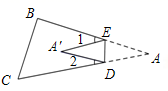
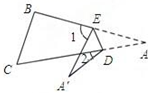
②当点 落在四边形
外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,
,
,
之间又存在什么关系?请说明.
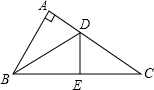
将三角形 纸片沿
折叠,使点A落在点
处.
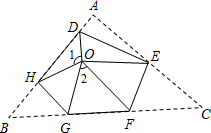
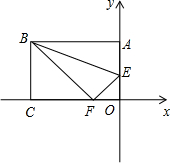
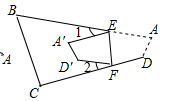
如图,若把四边形 纸片沿
折叠,使点A、D落在四边形
的内部点
、
的位置,请你探索此时
,
,
,
之间的数量关系,写出你发现的结论,并说明理由.
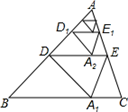
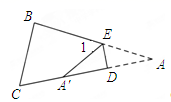
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.

探究发现
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为.
小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.