B .
B .  C .
C .  D .
D . 
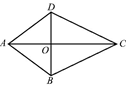
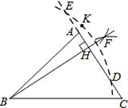
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;②作射线BF , 交边AC于点H;③以B为圆心,BK长为半径作弧,交直线AC于点D和E;④取一点K使K和B在AC的两侧;所以BH就是所求作的高.其中顺序正确的作图步骤是( )
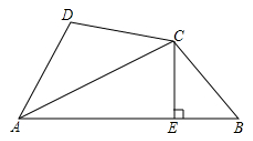

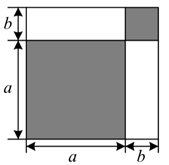
方法1:;方法2:.
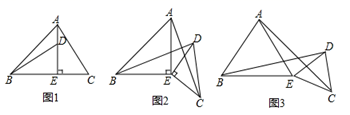
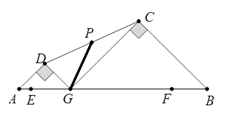
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC所成的角的度数吗?如果能,请直接写出该角的度数;如果不能,请说明理由.