江苏省无锡市滨湖区2021届九年级上学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：146 类型：期末考试

一、单选题

1. (2021九上·滨湖期末) 下列方程有实数根的是（）

A . x²＋x＋1＝0 B . x²－x－1＝0 C . x²－2x＋3＝0 D . x²－ $\text{[math]}$ x＋1＝0

答案解析收藏纠错 + 选题
2. (2021九上·滨湖期末) 一个不透明的盒子中装有4个形状、大小质地完全相同的小球，这些小球上分别标有－1、0、2和3.从中随机摸取一个小球，则这个小球所标数字是正数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·滨湖期末) 对于一组数据－1，2，－1， 4，下列结论不正确的是（）

A . 平均数是1 B . 众数是－1 C . 中位数是1.5 D . 方差是4.5

答案解析收藏纠错 + 选题
4. (2024九上·潮南月考) 抛物线y=（x＋2）²＋1的对称轴是（）

A . 直线x＝－1 B . 直线x＝1 C . 直线x＝2 D . 直线x＝－2

答案解析收藏纠错 + 选题
5. (2022九上·永春期中) 生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下a与全身 $\text{[math]}$ 的高度比值接近0.618，可以增加视觉美感，若图中 $\text{[math]}$ 为2米，则a约为（）

A . 1.24米 B . 1.38米 C . 1.42米 D . 1.62米

答案解析收藏纠错 + 选题
6. (2021九上·滨湖期末) 如图是小刘做的一个风筝支架示意图，已知BC∥PQ，AB：AP=2：5，AQ=20cm，则CQ的长是（）

A . 8cm B . 12cm C . 30cm D . 50cm

答案解析收藏纠错 + 选题
7. (2021九上·浦口月考) 二次函数y=x²－(m－1)x+4的图象与x轴有且只有一个交点，则m的值为（）

A . 1或－3 B . 5或－3 C . －5或3 D . 以上都不对

答案解析收藏纠错 + 选题
8. (2021九上·滨湖期末) 有一个三角形木架三边长分别是15cm，20cm，24cm，现要再做一个与其相似的三角形木架，而只有长为12cm和24cm的两根木条.要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有（）

A . 一种 B . 两种 C . 三种 D . 四种

答案解析收藏纠错 + 选题
9. (2021九上·滨湖期末) 如图，在扇形BOC中，∠BOC＝60°，点D为弧BC的中点，点E为半径OB上一动点，若OB＝2，则阴影部分周长的最小值为（）

A . 2＋ $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ ＋ $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ ＋ $\text{[math]}$ D . 2 $\text{[math]}$ ＋ $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·兰州模拟) 已知二次函数y＝ax²＋bx＋c的顶点D（－1，2），与x轴的一个交点A在（－3，0）和（－2，0）之间（不含端点），如图所示，有以下结论：①b²－4ac＞0；②a＋b＋c＜0；③c－a＝2；④方程ax²＋bx＋c－2＝0有两个相等的实数根，其中结论正确的个数有（）

A . 1个 B . 2 个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·诸暨期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
12. (2021九上·滨湖期末) 想了解中央电视台《开学第一课》的收视率，适合的调查方式为.（填“普查”或“抽样调查”）

答案解析收藏纠错 + 选题
13. (2021九上·滨湖期末) 某小区今年2月份绿化面积为6400m² ，到了今年4月份增长到8100m² ，假设绿化面积月平均增长率都相同，则增长率为．

答案解析收藏纠错 + 选题
14. (2021·龙岗模拟) 若甲、乙、丙、丁4名同学3次数学成绩的平均分都是96分，它们的方差分别是S_甲²＝3.6，S_乙²＝4.6，S_丙²＝6.3 ，S_丁²＝7.3，则这4名同学3次数学成绩最稳定的是.

答案解析收藏纠错 + 选题
15. (2021九上·浦口月考) 若圆锥的母线为10，底面半径为6，则圆锥的侧面积为．

答案解析收藏纠错 + 选题
16. (2021九上·浦口月考) 设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R和r，则R—r =.

答案解析收藏纠错 + 选题
17. (2021九上·滨湖期末) 如图，C、D是半圆O上两点，AB是直径，若AD＝CD＝2，CB＝4，则半圆的半径为.

答案解析收藏纠错 + 选题
18. (2021九上·滨湖期末) 在平面直角坐标系xOy中，设点P的坐标为（n－1，3n＋2），点Q是抛物线y=－x²＋x＋1上一点，则P，Q两点间距离的最小值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九上·滨湖期末) 解方程：
1. （1） x²＋4x－1＝0；
2. （2） x²＋10＝7x.
答案解析收藏纠错 + 选题
20. (2020九上·庆阳月考) 已知关于x的一元二次方程x²﹣6x+2m+1=0有实数根．
1. （1）求实数m的取值范围；
2. （2）若方程的两个实数根为x₁ ， x₂ ，且x₁x₂+x₁+x₂=15，求m的值．
答案解析收藏纠错 + 选题
21. (2021九上·滨湖期末) 甲、乙两个家庭准备到美丽的太湖景区游玩，各自随机选择到“灵山”、“拈花湾”、“鼋头渚”三个景点旅游.假设上述三个景点中的每一个景点被选到的可能性相同.
1. （1）求甲家庭选择到“拈花湾”旅游的概率；
2. （2）求甲、乙两个家庭选择到上述三个景点中的同一个景点旅游的概率.（用列表法或树状图法）
答案解析收藏纠错 + 选题

22. (2021九上·滨湖期末) 在新冠肺炎疫情期间，某市防控指挥部想了解各学校教职工参与志愿服务的情况.在全市各学校随机调查了部分参与志愿服务的教职工，对他们的志愿服务时间进行统计，整理并绘制成两幅不完整的统计图表.请根据两幅统计图表中的信息回答下列问题：

	志愿服务时间（小时）	频数
A	0＜x≤30	a
B	30＜x≤60	10
C	60＜x≤90	16
D	90＜x≤120	20

（1）本次被抽取的教职工共有名；
（2）表中a＝，扇形统计图中“C”部分所占百分比为%；
（3）扇形统计图中，“D”所对应的扇形圆心角的度数为°；
（4）若该市共有30000名教职工参与志愿服务，那么志愿服务时间多于60小时的教职工大约有多少人？

答案解析收藏纠错 + 选题

23. (2021九上·滨湖期末) 如图，在边长为1小正方形的网格中，△ABC的顶点A、B、C均落在格点上，请用无刻度的直尺按要求作图.（保留画图痕迹，不需证明）
1. （1）如图①，点P在格点上，在线段AB上找出所有符合条件的点Q，使△APQ和△ABC相似；
2. （2）如图②，在AC上作一点M，使以M为圆心，MC为半径的⊙M与AB相切，并直接写出此时⊙M的半径为.
答案解析收藏纠错 + 选题
24. (2021九上·滨湖期末) 如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E，交AD于点F，交CD的延长线于点G.
1. （1）求证：△ABE∽△CGE；
2. （2）若AF＝2FD，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2021九上·滨湖期末) 如图，AB是⊙O的一条弦，点C是⊙O外一点， OC⊥OA，OC交AB于点P、交⊙O于点Q，且CP＝CB＝2.
1. （1）求证：BC是⊙O的切线；
2. （2）若∠A＝22.5°，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
26. (2021九上·滨湖期末) 我区“绿色科技公司”研发了一种新产品，该产品的成本为每件3000元.在试销期间，营销部门建议：①购买不超过10件时，每件销售价为3600元；②购买超过10件时，每多购买一件，所购产品的销售单价均降低5元，但最低销售单价为3200元.根据以上信息解决下列问题：
1. （1）直接写出：购买这种产品件时，销售单价恰好为3200元；
2. （2）设购买这种产品x件（其中x＞10，且x为整数），该公司所获利润为y元，求y与x之间的函数表达式；
3. （3）在试销期间销售人员发现：当购买产品的件数超过10件时，会出现随着数量的增多，公司所获利润反而减少这一情况.为使销售数量越多，公司所获利润越大，公司应将最低销售单价调整为多少元？（其它销售条件不变）
答案解析收藏纠错 + 选题
27. (2021九上·滨湖期末) 如图，平面直角坐标系xOy中，矩形OABC如图放置，点B（4，3），E，F分别为OA，BC边上的中点，动点P从点 $\text{[math]}$ 出发以每秒2个单位速度沿EO方向向点O运动，同时，动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时，另一个点随之停止.连接EF、PQ，且EF与PQ相交于点M，连接AM.
1. （1）求线段AM的长度；
2. （2）过点A作AH⊥PQ，垂足为点 $\text{[math]}$ ，连接CH，求线段CH长度的最小值.
答案解析收藏纠错 + 选题
28. (2021九上·滨湖期末) 已知二次函数y＝ax²－4ax＋c（a≠0）的图象与x轴的负半轴和正半轴分别交于A、B两点，与y轴交于点C，且△CAO和△BOC的面积之比为1∶3.
1. （1）求A点的坐标；（直接写出答案）
2. （2）若点C的坐标为（0，2c－2 ）.
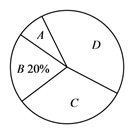
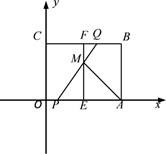
  ①求二次函数的解析式；
  
  ②设点C关于x轴的对称点为C′，连接C′B，在线段C′B上是否存在一点P，使∠CPC′＝3∠CBO，若存在，求点P的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题