
 B .
B .  C .
C .  D .
D . 

①若点P(﹣3,m),Q(3,n)在抛物线上,则m<n;②c=a+3;③a+b+c<0;④方程ax2+bx+c=3有两个相等的实数根.




频数分布表
|
学习时间分组 |
频数 |
频率 |
|
A组( | 9 | m |
| B组( | 18 | 0.3 |
| C组( | 18 | 0.3 |
| D组( | n | 0.2 |
| E组( | 3 | 0.05 |


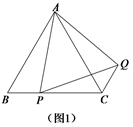


求证:四边形 是对余四边形;

