江苏省无锡市宜兴市和桥联盟2021年数学中考模拟试卷（3月）

更新时间：2021-07-10 浏览次数：114 类型：中考模拟

一、单选题

1. (2020七上·长沙期末) -2的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2021·宜兴模拟) 函数 $\text{[math]}$ 中自变量 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·吴桥期末) sin60°=（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·宜兴模拟) 下列图标中，既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022·惠山模拟) 如图，左图是由4个大小相同的正方体组合而成的几何体，其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021·广陵模拟) 已知某圆锥的底面半径为3cm，母线长5cm，则它的侧面展开图的面积为（）

A . 30cm² B . 15cm² C . 30πcm² D . 15πcm²

答案解析收藏纠错 + 选题
7. (2021·宜兴模拟) 新冠疑似病例需在定点医院隔离观察，要掌握他在一周内的体温是否稳定，则医生需要了解这位病人7天体温的（）

A . 中位数 B . 平均数 C . 方差 D . 众数

答案解析收藏纠错 + 选题
8. (2024八下·重庆市月考) 下列命题中，真命题是（）

A . 对角线相等的四边形是矩形 B . 对角线互相垂直平分的四边形是菱形 C . 一组对边平行，另一组对边相等的四边形是平行四边形 D . 一组邻边相等，并且有一个内角为直角的四边形是正方形

答案解析收藏纠错 + 选题
9. (2021·宜兴模拟) 如图，曲线 $\text{[math]}$ 是抛物线 $\text{[math]}$ 的一部分（其中 $\text{[math]}$ 是抛物线与 $\text{[math]}$ 轴的交点， $\text{[math]}$ 是顶点），曲线 $\text{[math]}$ 是双曲线 $\text{[math]}$ 的一部分.曲线 $\text{[math]}$ 与 $\text{[math]}$ 组成图形 $\text{[math]}$ .由点 $\text{[math]}$ 开始不断重复图形 $\text{[math]}$ 形成一组“波浪线”.若点 $\text{[math]}$ ， $\text{[math]}$ 在该“波浪线”上，则 $\text{[math]}$ 的最大值为（）

A . 5 B . 6 C . 2020 D . 2021

答案解析收藏纠错 + 选题
10. (2022九上·温州月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，将矩形沿 $\text{[math]}$ 翻折，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边 $\text{[math]}$ 处，连接 $\text{[math]}$ ，在 $\text{[math]}$ 上取点 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作⊙O与 $\text{[math]}$ 相切于点 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论：① $\text{[math]}$ 是 $\text{[math]}$ 的中点；②⊙O的半径是2；③ $\text{[math]}$ ；④S_阴影 $\text{[math]}$ .其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2021·南山模拟) 因式分解：3x²﹣12＝．

答案解析收藏纠错 + 选题
12. (2021·宜兴模拟) 电影《流浪地球》中，人类计划带着地球一起逃到距地球4光年的半人马星座比邻星.已知光年是天文学中的距离单位，4光年大约是381000亿千米，该数据用科学记数法表示为亿千米.

答案解析收藏纠错 + 选题
13. (2021·宜兴模拟) 已知正多边形的一个外角为72°，则该正多边形的内角和为.

答案解析收藏纠错 + 选题
14. (2021·宜兴模拟) 写出一个 $\text{[math]}$ 关于 $\text{[math]}$ 的函数关系式：满足在第一象限内， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大的函数是.

答案解析收藏纠错 + 选题
15. (2021·宜兴模拟) 如图，已知 $\text{[math]}$ 的直径为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在 $\text{[math]}$ 上，且 $\text{[math]}$ ，则 $\text{[math]}$ 长.

答案解析收藏纠错 + 选题
16. (2021·宜兴模拟) 如图，菱形 $\text{[math]}$ 的边 $\text{[math]}$ 轴，垂足为点 $\text{[math]}$ ，顶点 $\text{[math]}$ 在第二象限，顶点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，反比例函数 $\text{[math]}$ 的图象同时经过顶点 $\text{[math]}$ 、 $\text{[math]}$ ，若点 $\text{[math]}$ 的横坐标为1， $\text{[math]}$ .则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
17. (2021·宜兴模拟) 如图，扇形 $\text{[math]}$ 中， $\text{[math]}$ ，将扇形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转，得到扇形 $\text{[math]}$ ，若点 $\text{[math]}$ 刚好落在弧 $\text{[math]}$ 上的点 $\text{[math]}$ 处，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题

三、解答题

18. (2021·宜兴模拟) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2021·宜兴模拟)
1. （1）解方程： $\text{[math]}$ ；
2. （2）解不等式组 $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2021·宜兴模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的对角线， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为 $\text{[math]}$ 、 $\text{[math]}$ .求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. (2022·揭阳模拟) 太仓人杰地灵，为了了解学生对家乡历史文化名人的知晓情况，某校对部分学生进行了随机抽样调查，并将调查结果绘制成如图所示统计图的一部分.

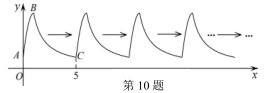
根据统计图中的信息，回答下列问题：
1. （1）本次抽样调查的样本容量是；
2. （2）在扇形统计图中，“了解很少”所在扇形的圆心角是度；
3. （3）若全校共有学生1300人，那么该校约有多少名学生“基本了解”太仓的历史文化名人？
答案解析收藏纠错 + 选题
22. (2021·徐州模拟) 2020春开学为防控冠状病毒，学生进校园必须戴口罩，测体温，江阴初级中学开通了三条人工测体温的通道，每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温（每个通道一位老师），周一有小卫和小孙两学生进校园，在3个人工测体温通道中，可随机选择其中的一个通过．
1. （1）求小孙进校园时，由王老师测体温的概率；
2. （2）求两学生进校园时，都是王老师测体温的概率．
答案解析收藏纠错 + 选题
23. (2021·宜兴模拟) 已知：如图，在△ABC中，AB＝AC，AE是∠BAC的平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径.
1. （1）求证：AE与⊙O相切；
2. （2）当BC＝6，cosC＝ $\text{[math]}$ 时，求⊙O的半径.
答案解析收藏纠错 + 选题
24. (2021·宜兴模拟) 城市内环高架能改善整个城市的交通状况.在一般情况下，高架上的车流速度 $\text{[math]}$ （单位：千米/小时）是车流密度 $\text{[math]}$ （单位：辆/千米）的函数.当高架上的车流密度达到188辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过28辆/千米时，车流速度为80千米/小时.研究表明：当 $\text{[math]}$ 时，车流速度 $\text{[math]}$ 是车流密度 $\text{[math]}$ 的一次函数.
1. （1）当 $\text{[math]}$ 时，求车流速度 $\text{[math]}$ 关于车流密度 $\text{[math]}$ 的函数解析式；
2. （2）若车流速度 $\text{[math]}$ 不低于50千米/小时，求车流密度 $\text{[math]}$ 为多大时，车流量 $\text{[math]}$ （单位时间内通过高架桥上某观测点的车辆数，单位：辆/小时）可以达到最大，并求出最大值.
答案解析收藏纠错 + 选题
25. (2021·宜兴模拟) 如图，在边长为1小正方形的网格中，△ABC的顶点A、B、C均落在格点上，请用无刻度的直尺按要求作图.（保留画图痕迹，不需证明）
1. （1）如图①，点P在格点上，在线段AB上找出所有符合条件的点Q，使△APQ和△ABC相似；
2. （2）如图②，在AC上作一点M，使以M为圆心，MC为半径的⊙M与AB相切，并直接写出此时⊙M的半径为 ▲ .
答案解析收藏纠错 + 选题
26. (2021·宜兴模拟) 如图，二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的右边），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .
1. （1）请直接写出 $\text{[math]}$ 、 $\text{[math]}$ 两点的坐标： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）若以 $\text{[math]}$ 为直径的圆恰好经过这个二次函数图象的顶点.
  ①求这个二次函数的表达式；
  
  ②若 $\text{[math]}$ 为二次函数图象位于第二象限部分上的一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 平行于 $\text{[math]}$ 轴，交直线 $\text{[math]}$ 于点 $\text{[math]}$ .连接 $\text{[math]}$ 、 $\text{[math]}$ ，是否存在一个点 $\text{[math]}$ ，使 $\text{[math]}$ ？如果存在，请求出点 $\text{[math]}$ 的坐标；如果不存在，请说明理由.
答案解析收藏纠错 + 选题
27. (2021·宜兴模拟) 将一矩形纸片 $\text{[math]}$ 放在直角坐标系中， $\text{[math]}$ 为原点， $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）如图1，在 $\text{[math]}$ 上取一点 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使 $\text{[math]}$ 点落至 $\text{[math]}$ 边上的 $\text{[math]}$ 点，求直线 $\text{[math]}$ 的解析式；
2. （2）如图2，在 $\text{[math]}$ 、 $\text{[math]}$ 边上选取适当的点 $\text{[math]}$ 、 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使 $\text{[math]}$ 点落在 $\text{[math]}$ 边上的 $\text{[math]}$ 点，过 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ 点，交 $\text{[math]}$ 于 $\text{[math]}$ 点.
  ①求证： $\text{[math]}$ ；
  
  ②设 $\text{[math]}$ ，探求 $\text{[math]}$ 与 $\text{[math]}$ 满足的等量关系式，并将 $\text{[math]}$ 用含 $\text{[math]}$ 的代数式表示（指出变量 $\text{[math]}$ 的取值范围）；
3. （3）在（2）的条件下，当 $\text{[math]}$ 时，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，问坐标轴上是否存在点 $\text{[math]}$ ，使以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形是平行四边形，若存在，请直接写出 $\text{[math]}$ 点坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题