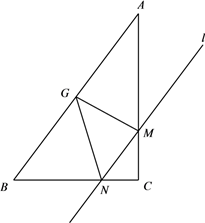

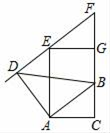



如图,在平面直角坐标系xOy中,直线y= x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为.
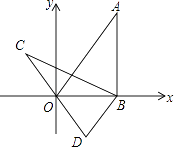
①∠ABN=60°;②AM=1;③QN= ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
.
其中正确结论的序号是.
问题背景:
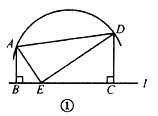
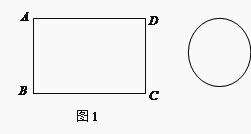
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:
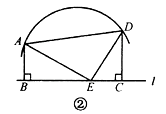
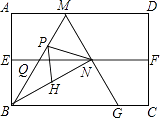
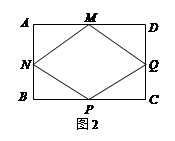
(1)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;
拓展迁移:
(1)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片;
①当BE=DF=时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .
如图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形,再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的两个矩形为“叠加矩形”.请完成下列问题: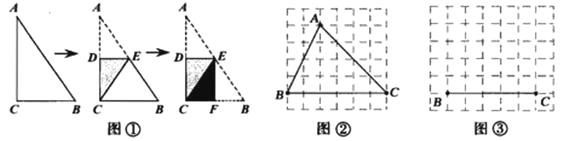
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形” 为正方形,那么它必须满足的条件是 .
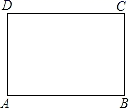
以下是小红的研究过程.
| 思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
| 折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分. |