山东省菏泽市牡丹区2021年中考数学二模试卷

更新时间：2021-07-27 浏览次数：135 类型：中考模拟

一、单选题

1. (2023七下·上思月考) 下列各数中，比3大比4小的无理数是（）

A . 3.14 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021八上·西峰期末) 目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为 $\text{[math]}$ （其中 $\text{[math]}$ ），用科学记数法表示这个最小刻度（单位：m），结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·莱芜期末) 如图所示的几何体，它的左视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·牡丹模拟) 如图，长方形ABCD中∠DAC＝68°，请依据尺规作图的痕迹，求出∠α等于（）

A . 34° B . 44° C . 56° D . 68°

答案解析收藏纠错 + 选题
5. (2024九上·钦州月考) 当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
6. (2020九上·临邑期末) 如图，AB是⊙O的直径，直线DE与⊙O相切于点C，过A，B分别作AD⊥DE，BE⊥DE，垂足为点D，E，连接AC，BC，若AD＝ $\text{[math]}$ ，CE＝3，则 $\text{[math]}$ 的长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ π C . $\text{[math]}$ π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
7. (2021·牡丹模拟) 如图，已知 $\text{[math]}$ 与 $\text{[math]}$ 位似，且 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比为1：2，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·牡丹模拟) 如图（1）所示，E为矩形 $\text{[math]}$ 的边 $\text{[math]}$ 上一点，动点 $\text{[math]}$ 同时从点B出发，点P沿折线 $\text{[math]}$ 运动到点C时停止，点Q沿 $\text{[math]}$ 运动到点C时停止，它们运动的速度都是 $\text{[math]}$ /秒．设 $\text{[math]}$ 同时出发t秒时， $\text{[math]}$ 的面积为 $\text{[math]}$ ．已知y与t的函数关系图象如图（2）（曲线 $\text{[math]}$ 为抛物线的一部分），则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④当 $\text{[math]}$ 秒时， $\text{[math]}$ ；其中正确的结论是（　　）

A . ①②③ B . ①③ C . ①③④ D . ②④

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·青岛模拟) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2021·牡丹模拟) 已知x，y都是实数，且y＝ $\text{[math]}$ + $\text{[math]}$ ﹣2，则y^x＝．

答案解析收藏纠错 + 选题
11. (2021·牡丹模拟) 若关于x的方程 $\text{[math]}$ 有增根，则m的值是

答案解析收藏纠错 + 选题
12. (2021·牡丹模拟) 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所在直线为反比例函数 $\text{[math]}$ 的对称轴，当反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 两点时，k的值为.

答案解析收藏纠错 + 选题
13. (2021·牡丹模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P为 $\text{[math]}$ 边上一点，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，点A落在点 $\text{[math]}$ 处，当点 $\text{[math]}$ 在矩形的对角线上时， $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
14. (2021·牡丹模拟) 如图， $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上，且 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，在射线 $\text{[math]}$ 上截取 $\text{[math]}$ ，使得 $\text{[math]}$ ；过点 $\text{[math]}$ 作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，在射线 $\text{[math]}$ 上截取 $\text{[math]}$ ，使得 $\text{[math]}$ ；……；按照此规律进行下去，则 $\text{[math]}$ 长为．

答案解析收藏纠错 + 选题

三、解答题

15. (2023九下·冷水滩模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021·牡丹模拟) 先化简，再求值： $\text{[math]}$ ，请从不等式组 $\text{[math]}$ 的整数解中选择一个合适的值代入求值．

答案解析收藏纠错 + 选题
17. (2021·牡丹模拟) 已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE＝CF ，点G ， H在对角线BD上，且BG＝DH ．
1. （1）求证：△BFH≌△DEG；
2. （2）连接DF ，若DF＝BF ，则四边形EGFH是什么特殊四边形？证明你的结论．
答案解析收藏纠错 + 选题
18. (2021·牡丹模拟)
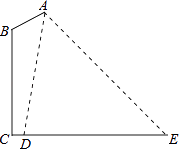
如图，在路边安装路灯，灯柱BC高15m，与灯杆AB的夹角ABC为120°．路灯采用锥形灯罩，照射范围DE长为18.9m，从D、E两处测得路灯A的仰角分别为∠ADE=80.5°，∠AED=45°．求灯杆AB的长度．（参考数据：cos80.5°≈0.2，tan80.5°≈6.0）

答案解析收藏纠错 + 选题
19. (2021·牡丹模拟) 第30届菏泽国际牡丹文化旅游节于4月1日至5月10日举办，主题为“赞盛世牡丹，品魅力菏泽”．为了宣传牡丹制品，某商店欲购进 $\text{[math]}$ 两种牡丹制品，若购进A种牡丹制品5件，B种牡丹制品3件，共需450元；若购进A种牡丹制品10件，B种牡丹制品8件，共需1000元．
1. （1）购进 $\text{[math]}$ 两种牡丹制品每件各需多少元？
2. （2）该商店购进足够多的 $\text{[math]}$ 两种牡丹制品，在销售中发现，A种牡丹制品售价为每件80元，每天可销售100件，现在决定对A种牡丹制品在每件80元的基础上降价销售，每件每降价1元，多售出20件，该商店对A种牡丹制品降价销售后每天销量超过200件；B种牡丹制品销售状况良好，每天可获利7000元，为使销售 $\text{[math]}$ 两种牡丹制品每天总获利为10000元，A种牡丹制品每件降价多少元？
答案解析收藏纠错 + 选题
20. (2021·牡丹模拟) 如图，在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C坐标为（-1，0），．一次函数 $\text{[math]}$ 的图象经过点B、C ，反比例函数 $\text{[math]}$ 的图象经过点B．
1. （1）求一次函数和反比例函数的关系式；
2. （2）直接写出当x＜0时， $\text{[math]}$ 的解集；
3. （3）在x轴上找一点M ，使得AM+BM的值最小，并求出点M的坐标和AM+BM的最小值．
答案解析收藏纠错 + 选题
21. (2021·牡丹模拟) “校园安全”受到全社会的关注，菏泽市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：
1. （1）接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为°；
2. （2）请补全条形统计图；
3. （3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；
4. （4）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．
答案解析收藏纠错 + 选题
22. (2022九下·达州月考) 如图，在 $\text{[math]}$ ABC中，∠C=90°．∠ABC的平分线交AC于点E ，点F在AB上，以BF为直径的⊙O恰好经过点E ．
1. （1）求证：AC是⊙O的切线；
2. （2）若AE=2AF=4，求BC的长．
答案解析收藏纠错 + 选题
23. (2021·牡丹模拟) 已知：如图1所示将一块等腰三角板BMN放置与正方形ABCD的 $\text{[math]}$ 重合，连接AN、CM，E是AN的中点，连接BE．
1. （1）（观察猜想）
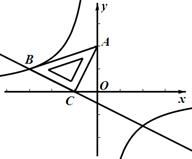
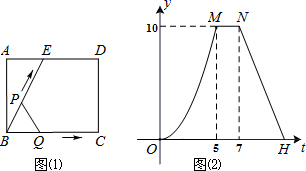
  CM与BE的数量关系是；CM与BE的位置关系是；
2. （2）（探究证明）
  如图2所示，把三角板BMN绕点B逆时针旋转 $\text{[math]}$ ，其他条件不变，线段CM与BE的关系是否仍然成立，并说明理由；
3. （3）（拓展延伸）
  若旋转角 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2021·牡丹模拟) 如图，抛物线y＝﹣x²+bx+c与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C
1. （1）求抛物线的表达式；
2. （2）如图1，若点F在线段OC上，且OF＝OA ，经入过点F的直线在第一象限内与抛物线交于点D ，与线段BC交于点E ，求 $\text{[math]}$ 的最大值；
3. （3）如图2，若P为抛物线的顶点，动点Q在抛物线上，当∠QCO＝∠PBC时，请直接写出点Q的坐标．
答案解析收藏纠错 + 选题