
 B .
B . 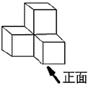
 B .
B .  C .
C .  D .
D . 


该地区每周接种疫苗人数统计表
|
周次 |
第1周 |
第2周 |
第3周 |
第4周 |
第5周 |
第6周 |
第7周 |
第8周 |
|
接种人数(万人) |
7 |
10 |
12 |
18 |
25 |
29 |
37 |
42 |
|
该地区全民接种疫苗情况扇形统计图 | A:建议接种疫苗已接种人群 B:建议接种疫苗尚未接种人群 C:暂不建议接种疫苗人群 | |||||||
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、
作一条直线(如图所示,该直线的函数表达式为
),那么这条直线可近似反映该地区接种人数的变化趋势.
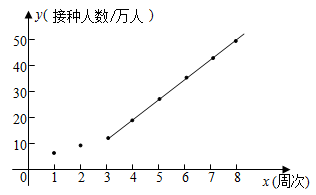
请根据以上信息,解答下列问题:
①估计第9周的接种人数约为 ▲ 万人;
②专家表示:疫苗接种率至少达60%,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
试根据下列各题中所给的定点 的坐标和角度
的大小来解决相关问题.
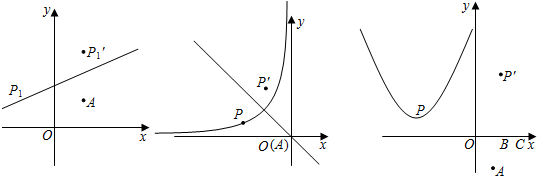
如图1,设 ,
,点
是一次函数
图像上的动点,已知该一次函数的图象经过点
.
点 旋转后,得到的点
的坐标为;
如图2,设 ,
,点
反比例函数
的图像上的动点,过点
作二、四象限角平分线的垂线,垂足为
,求
的面积.
如图3,设A ,
,点
是二次函数
图像上的动点,已知点
、
,试探究
的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.