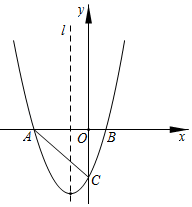
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
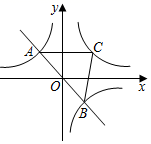
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
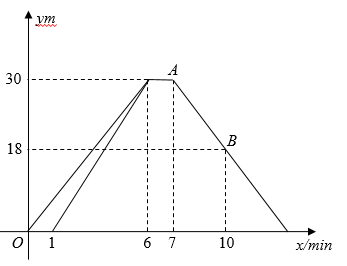
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:

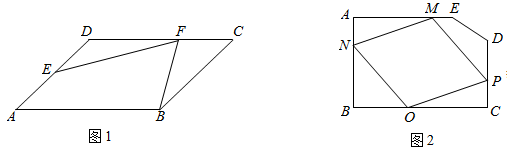
如图1,在 中,
,
,
,E是
的中点,点F在
上且
求四边形
的面积.(结果保留根号)
某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园 按设计要求,要在五边形河畔公园
内挖一个四边形人工湖
,使点O、P、M、N分别在边
、
、
、
上,且满足
,
.已知五边形
中,
,
,
,
,
.满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖
?若存在,求四边形
面积的最小值及这时点
到点
的距离;若不存在,请说明理由.

| 型号 | | | |
| 单价(元/袋) | 30 | 35 | 40 |
若购买 型口罩的数量是
型的2倍,设购买
型口罩
袋,该企业购买口罩的总费用为
元.
|
成本(元/棵) |
产量(kg/棵) |
|
|
苹果树 |
120 |
30 |
|
桔子树 |
80 |
25 |
设种植苹果树x棵.

|
里程/千米 |
收费/元 |
|
2千米以下(含2千米) |
11.4 |
|
2千米以上,每增加1千米 |
1.95 |