山东省烟台市2021年中考数学试卷

更新时间：2024-07-13 浏览次数：431 类型：中考真卷

一、单选题

1. (2021七上·柳江月考) 若x的相反数是3，则x的值是（）

A . -3 B . $\text{[math]}$ C . 3 D . ±3

答案解析收藏纠错 + 选题
2. (2022·鄂伦春模拟) 下列数学符号中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·乐陵月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九下·龙凤期中) 一个正方体沿四条棱的中点切割掉一部分后，如图所示，则该几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·烟台) 2021年5月15日，天问一号探测器成功着陆火星，迈出了我国星际探测征程的重要一步．已知火星与地球的近距离约为5500万公里，5500万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·长春模拟) 一副三角板如图就置，两三角板的斜边互相平行，每个三角板的直角顶点都在另一个三角板的斜边上，图中 $\text{[math]}$ 的度数为（）

A . 45° B . 60° C . 75° D . 85°

答案解析收藏纠错 + 选题
7. (2023八下·长沙期中) 如图，在直角坐标系中，菱形 $\text{[math]}$ 的顶点A ， B ， C在坐标轴上，若点B的坐标为 $\text{[math]}$ ， $\text{[math]}$ ，则点D的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 如图所示，若用我们数学课本上采用的科学计算器进行计算，其按键顺序及结果如下：
按键的结果为m；

按键的结果为n；

按键的结果为k．

下列判断正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021九上·台安月考) 已知关于x的一元二次方程 $\text{[math]}$ ，其中m ， n在数轴上的对应点如图所示，则这个方程的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
10. (2022·黄陂自主招生) 连接正六边形不相邻的两个顶点，并将中间的六边形涂成黑色，制成如图所示的镖盘．将一枚飞镖任意投掷到镖盘上，飞镖落在黑色区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024九下·福田开学考) 如图，二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴交于点C ．下列结论：
① $\text{[math]}$ ；②当 $\text{[math]}$ 时，y随x的增大而增大；③ $\text{[math]}$ ；④ $\text{[math]}$ ．

其中正确的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
12. (2021九上·蔡甸月考) 由12个有公共顶点O的直角三角形拼成的图形如图所示， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2022·黄埔模拟) 若 $\text{[math]}$ 在实数范围内有意义，则x的取值范围为．

答案解析收藏纠错 + 选题
14. (2023·吉林模拟) 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆 $\text{[math]}$ ，从木杆的顶端B观察井水水岸D ，视线 $\text{[math]}$ 与井口的直径 $\text{[math]}$ 交于点E ，如果测得 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，那么 $\text{[math]}$ 为米．

答案解析收藏纠错 + 选题
15. (2022·顺义模拟) 幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1~9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a的值为．

答案解析收藏纠错 + 选题
16. (2021·烟台) 数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为40米，当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为30°，则旗杆的高度约为米．（结果精确到1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
17. (2022·枣庄模拟) 如图，在正方形网格中，每个小正方形的边长都是1， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，点A ， B ， O在网格线的交点上，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
18. (2021·烟台) 综合实践活动课上，小亮将一张面积为 $\text{[math]}$ ，其中一边 $\text{[math]}$ 为8cm的锐角三角形纸片（如图1），经过两刀裁剪，拼成了一个无缝隙、无重叠的矩形 $\text{[math]}$ （如图2），则矩形的周长为cm．

答案解析收藏纠错 + 选题

三、解答题

19. (2024九下·连云港月考) 先化简，再求值： $\text{[math]}$ ，从 $\text{[math]}$ 中选出合适的x的整数值代入求值．

答案解析收藏纠错 + 选题

20. (2022九上·长顺期末) 2021年是中国共产党成立100周年，为普及党史知识，培养爱国主义精神，今年五月份，某市党校举行党史知识竞赛，每个班级各选派15名学员参加了网上测试，现对甲、乙两班学员的分数进行整理分析如下：

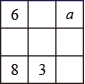
甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98．

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89．

（1）按如下分数段整理两班测试成绩

班级	70.5~75.5	75.5~80.5	80.5~85.5	85.5~90.5	90.5~95.5	95.5~100.5
甲	1	2	a	5	1	2
乙	0	3	3	6	2	1

表中 $\text{[math]}$ ；

（2）补全甲班15名学员测试成绩的频数分布直方图；

（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

班级	平均数	众数	中位数	方差
甲	86	$\text{[math]}$	86	44.8
乙	86	88	y	36.7

表中 $\text{[math]}$ ， $\text{[math]}$ ．

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是班；
（5）本次测试两班的最高分都是98分，其中甲班2人，乙班1人．现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，利用树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率．

答案解析收藏纠错 + 选题

21. (2022八下·长子期中) 如图，正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点A ，过点A作 $\text{[math]}$ 轴于点B ， $\text{[math]}$ ，点C在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ．
1. （1）求k的值及线段 $\text{[math]}$ 的长；
2. （2）点P为B点上方y轴上一点，当 $\text{[math]}$ 与 $\text{[math]}$ 的面积相等时，请求出点P的坐标．
答案解析收藏纠错 + 选题
22. (2022八下·南岗期末) 直播购物逐渐走进了人们的生活．某电商在抖音上对一款成本价为40元的小商品进行直播销售，如果按每件60元销售，每天可卖出20件．通过市场调查发现，每件小商品售价每降低5元，日销售量增加10件．
1. （1）若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？
2. （2）小明的线下实体商店也销售同款小商品，标价为每件62.5元．为提高市场竞争力，促进线下销售，小明决定对该商品实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？
答案解析收藏纠错 + 选题
23. (2021·烟台) 如图，已知 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）请按如下要求完成尺规作图．（不写作法，保留作图痕迹）
  ① $\text{[math]}$ 的角平分线 $\text{[math]}$ ，交 $\text{[math]}$ 于点D；
  
  ②作线段 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点O；
  
  ③以点O为圆心，以 $\text{[math]}$ 长为半径画圆，交边 $\text{[math]}$ 于点M．
2. （2）在（1）的条件下求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
24. (2022九上·龙亭月考) 有公共顶点A的正方形 $\text{[math]}$ 与正方形 $\text{[math]}$ 按如图1所示放置，点E ， F分别在边 $\text{[math]}$ 和 $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ，M是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点N．
1. （1）（观察猜想）
  线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是，位置关系是；
2. （2）（探究证明）
  将图1中的正方形 $\text{[math]}$ 绕点A顺时针旋转45°，点G恰好落在边 $\text{[math]}$ 上，如图2，其他条件不变，线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系是否仍然成立？并说明理由．
答案解析收藏纠错 + 选题
25. (2022·平阴模拟) 如图，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴正半轴交于点C ，且 $\text{[math]}$ ．抛物线的顶点为D ，对称轴交x轴于点E．直线 $\text{[math]}$ 经过B ， C两点．
1. （1）求抛物线及直线 $\text{[math]}$ 的函数表达式；
2. （2）点F是抛物线对称轴上一点，当 $\text{[math]}$ 的值最小时，求出点F的坐标及 $\text{[math]}$ 的最小值；
3. （3）连接 $\text{[math]}$ ，若点P是抛物线上对称轴右侧一点，点Q是直线 $\text{[math]}$ 上一点，试探究是否存在以点E为直角顶点的 $\text{[math]}$ ，且满足 $\text{[math]}$ ．若存在，求出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题