2021-2022学年北师版数学八年级上册期末模拟试题二

更新时间：2021-12-06 浏览次数：180 类型：期末考试

一、单选题

1. (2024九下·麦积模拟) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·贵阳) 今年是三年禁毒“大扫除”攻坚克难之年.为了让学生认识毒品的危害，某校举办了禁毒知识比赛，小红所在班级学生的平均成绩是80分，小星所在班级学生的平均成绩是85分，在不知道小红和小星成绩的情况下，下列说法比较合理的是（）

A . 小红的分数比小星的分数低 B . 小红的分数比小星的分数高 C . 小红的分数与小星的分数相同 D . 小红的分数可能比小星的分数高

答案解析收藏纠错 + 选题
3. (2024七下·大洼月考) 我国古代数学古典名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量，木条还剩余1尺；问长木多少尺？如果设木条长为x尺，绳子长为y尺，则下面所列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·印江月考) 如图，将一副三角板在平行四边形ABCD中作如下摆放，设 $\text{[math]}$ ，那么 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·路北期中) 实数 $\text{[math]}$ 在数轴上的对应点可能是（）

A . $\text{[math]}$ 点 B . $\text{[math]}$ 点 C . $\text{[math]}$ 点 D . $\text{[math]}$ 点

答案解析收藏纠错 + 选题
6. 计算： $\text{[math]}$ （）

A . 0 B . 1 C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八上·台儿庄期中) 如图，从一个大正方形中截去面积为 $\text{[math]}$ 和 $\text{[math]}$ 的两个小正方形，若随机向大正方形内投一粒米，则米粒落在图中阴影部分的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八上·东乡区期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·潍坊) 如图，一束水平光线照在有一定倾斜角度的平面镜上，若入射光线与出射光线的夹角为60°，则平面镜的垂线与水平地面的夹角α的度数是（）

A . 15° B . 30° C . 45° D . 60°

答案解析收藏纠错 + 选题
10. (2022八上·埇桥期中) 正比例函数y=kx（k≠0）的函数值y随着x增大而减小，则一次函数y=x+k的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
11. (2020九上·湛江开学考) 鄂尔多斯动物园内的一段线路如图1所示，动物园内有免费的班车，从入口处出发，沿该线路开往大象馆，途中停靠花鸟馆（上下车时间忽略不计），第一班车上午9：20发车，以后每隔10分钟有一班车从入口处发车，且每一班车速度均相同．小聪周末到动物园游玩，上午9点到达入口处，因还没到班车发车时间，于是从入口处出发，沿该线路步行25分钟后到达花鸟馆，离入口处的路程y（米）与时间x（分）的函数关系如图2所示，下列结论错误的是（）

A . 第一班车离入口处的距离y（米）与时间x（分）的解析式为y＝200x﹣4000（20≤x≤38） B . 第一班车从入口处到达花鸟馆所需的时间为10分钟 C . 小聪在花鸟馆游玩40分钟后，想坐班车到大象馆，则小聪最早能够坐上第四班车 D . 小聪在花鸟馆游玩40分钟后，如果坐第五班车到大象馆，那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟（假设小聪步行速度不变）

答案解析收藏纠错 + 选题
12. (2024九下·抚顺模拟) 我市在落实国家“精准扶贫”政策的过程中，为某村修建一条长为400米的公路，由甲、乙两个工程队负责施工.甲工程队独立施工2天后，乙工程队加入两工程队联合施工3天后，还剩50米的工程.已知甲工程队每天比乙工程队多施工2米，求甲、乙工程队每天各施工多少米？设甲工程队每天施工 $\text{[math]}$ 米，乙工程队每天施工 $\text{[math]}$ 米，根据题意，所列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2023八下·宿迁期末) 将直线 $\text{[math]}$ 向左平移 $\text{[math]}$ （ $\text{[math]}$ ）个单位后，经过点(1，−3)，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2020八上·普宁期中) 以水平数轴的原点 $\text{[math]}$ 为圆心过正半轴 $\text{[math]}$ 上的每一刻度点画同心圆，将 $\text{[math]}$ 逆时针依次旋转 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 得到 $\text{[math]}$ 条射线，构成如图所示的“圆”坐标系，点 $\text{[math]}$ 、 $\text{[math]}$ 的坐标分别表示为 $\text{[math]}$ 、 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标表示为.

答案解析收藏纠错 + 选题
15. (2021七下·二道期末) 已知x、y满足方程组 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
16. (2021·眉山) 观察下列等式： $\text{[math]}$ ；
$\text{[math]}$ ；

$\text{[math]}$ ；

……

根据以上规律，计算 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2023九上·青秀期末) 在直角坐标系中，点A₁从原点出发，沿如图所示的方向运动，到达位置的坐标依次为：A₂（1，0），A₃（1，1），A₄（﹣1，1），A₅（﹣1，﹣1），A₆（2，﹣1），A₇（2，2），…．若到达终点A_n（506，﹣505），则n的值为．

答案解析收藏纠错 + 选题
18. (2022八下·启东月考) 如图，在正方形 ABCD ，E是对角线 BD 上一点， AE 的延长线交 CD 于点F ，连接 CE ．若∠BAE=56° ，则 ∠CEF= ° ．

答案解析收藏纠错 + 选题

三、解答题

19. (2021八上·沈阳期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2021八上·浦东期中) 计算：﹣ $\text{[math]}$ ÷（2 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
21. (2021七下·新抚期末) 解方程组：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2021·大庆) 某校要从甲，乙两名学生中挑选一名学生参加数学竞赛，在最近的8次选拔赛中，他们的成绩（成绩均为整数，单位：分）如下：
甲：92，95，96，88，92，98，99，100

乙：100，87，92，93，9▆，95，97，98

由于保存不当，学生乙有一次成绩的个位数字模糊不清，
1. （1）求甲成绩的平均数和中位数；
2. （2）求事件“甲成绩的平均数大于乙成绩的平均数”的概率；
3. （3）当甲成绩的平均数与乙成绩的平均数相等时，请用方差大小说明应选哪个学生参加数学竞赛．
答案解析收藏纠错 + 选题

23. (2021·宁波) 某通讯公司就手机流量套餐推出三种方案，如下表：

	A方案	B方案	C方案
每月基本费用（元）	20	56	266
每月免费使用流量（兆）	1024	m	无限
超出后每兆收费（元）	n	n

A，B，C三种方案每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系如图所示.

（1）请直接写出m，n的值.
（2）在A方案中，当每月使用的流量不少于1024兆时，求每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系式.
（3）在这三种方案中，当每月使用的流量超过多少兆时，选择C方案最划算？

答案解析收藏纠错 + 选题

24. (2021·襄阳) 为了切实保护汉江生态环境，襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后，某水库自然生态养殖的鱼在市场上热销，经销商老李每天从该水库购进草鱼和鲢鱼进行销售，两种鱼的进价和售价如下表所示：

	进价（元/斤）	售价（元/斤）
鲢鱼	$\text{[math]}$	5
草鱼	$\text{[math]}$	销量不超过200斤的部分	销量超过200斤的部分
		8	7

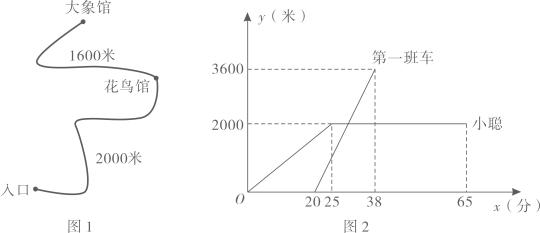
已知老李购进10斤鲢鱼和20斤草鱼需要155元，购进20斤鲢鱼和10斤草鱼需要130元.

（1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
（2）老李每天购进两种鱼共300斤，并在当天都销售完，其中销售鲢鱼不少于80斤且不超过120斤，设每天销售鲢鱼 $\text{[math]}$ 斤（销售过程中损耗不计）.
①分别求出每天销售鲢鱼获利 $\text{[math]}$ （元），销售草鱼获利 $\text{[math]}$ （元）与 $\text{[math]}$ 的函数关系式，并写出 $\text{[math]}$ 的取值范围；

②端午节这天，老李让利销售，将鲢鱼售价每斤降低 $\text{[math]}$ 元，草鱼售价全部定为7元斤，为了保证当天销售这两种鱼总获利 $\text{[math]}$ （元）的最小值不少于320元，求 $\text{[math]}$ 的最大值.

答案解析收藏纠错 + 选题

25. (2020·荆门) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于D， $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点E， $\text{[math]}$ 交 $\text{[math]}$ 于点F.
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
26. (2017·兰州)
如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．
1. （1）求证：△BDF是等腰三角形；
2. （2）
  如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．
  ①判断四边形BFDG的形状，并说明理由；
  ②若AB=6，AD=8，求FG的长．
答案解析收藏纠错 + 选题