


![]()
②在点P由点A到点B的运动过程中,点P表示的有理数为.(用含t的代数式表示)
⑴一次性购物不超过100元不享受优惠;
⑵一次性购物超过100元但不超过300元一律9折;
⑶一次性购物超过300元一律8折.
小李两次购物分别付款85元,252元,如果他一次性购买以上两次相同的商品,他应付款元.

![]()
![]()
①数轴上表示1和6的两点之间的距离是;
②数轴上表示﹣2和7的两点之间的距离是;
③数轴上表示﹣9和﹣3的两点之间的距离是.
数a和数b的两点之间的距离可以表示为.
如果数a和3的两点之间的距离是15,则可记为:|a﹣3|=15,那么a的值为多少.
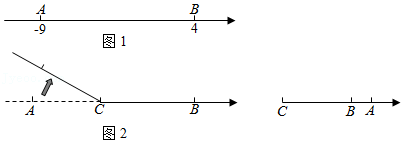
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

回答下列问题:
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小明在一条长方形纸带上画了一条数轴,进行如下操作探究:
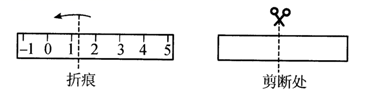
①当n<9时,售价为 元/千克;
②当n>9时,售价为 元/千克;
方案一:降价5%,并减免全部运费;方案二:降价8%,但运费不减.
请你帮小蓓计算哪种优惠方案更加合算.




|
优惠 条件 |
一次性购物 不超过200元 |
一次性购物超过200 元,但不超过600元 |
一次性购物 超过600元 |
|
优惠 办法 |
没有 优惠 |
全部按九折 优惠 |
其中600元扔按九折优惠, 超过600元部分按八折优惠 |
用代数式表示(所填结果需化简):
实际付款为元;当原价x超过600元时,实际付款为元.
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过500元 |
售价一律打九折 |
|
超过500元 |
售价一律打八折 |
按上述优惠条件,若小张第一天只购买甲种商品一次性付款210元,第二天只购买乙种商品打折后一次性付款440元,那么这两天他在该超市购买甲、乙两种商品一共多少件?

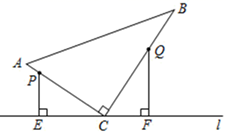
①当∠MEP=15°时,求∠EPN的度数;
②当EM∥PN时,直接写出t的值.