（鲁教版）2022-2023学年度第一学期七年级数学1.5 ...

更新时间：2022-08-09 浏览次数：72 类型：同步测试

一、单选题

1. (2022·河北) 题目：“如图，∠B＝45°，BC＝2，在射线BM上取一点A ，设AC＝d ，若对于d的一个数值，只能作出唯一一个△ABC ，求d的取值范围．”对于其答案，甲答： $\text{[math]}$ ，乙答：d＝1.6，丙答： $\text{[math]}$ ，则正确的是（）

A . 只有甲答的对 B . 甲、丙答案合在一起才完整 C . 甲、乙答案合在一起才完整 D . 三人答案合在一起才完整

答案解析收藏纠错 + 选题
2. (2022·禅城模拟) 一块三角形玻璃不慎被小明摔成了四片碎片（如图所示），小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店，就可以让师傅配一块与原玻璃一样的玻璃．你认为下列四个答案中考虑最全面的是（）

A . 带其中的任意两块去都可以 B . 带1、4或2、3去就可以了 C . 带1、4或3、4去就可以了 D . 带1、2或2、4去就可以了

答案解析收藏纠错 + 选题
3. 如图，AB，BC，CD，DE是四根长度均为5cm的火柴棒，点A，C，E共线，若AC=6cm，CD⊥BC，则线段CE的长度是（）

A . 6cm B . 7cm C . 6 $\text{[math]}$ cm D . 8cm

答案解析收藏纠错 + 选题
4. (2021八上·莒南期中) 如图，在 $\text{[math]}$ 的网格中，每一个小正方形的边长都是1，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在格点上，连接 $\text{[math]}$ ， $\text{[math]}$ 相交于 $\text{[math]}$ ，那么 $\text{[math]}$ 的大小是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八上·长沙期中) 如图，点C在线段BD上，AB⊥BD于B，ED⊥BD于D.∠ACE=90°，且AC=5cm，CE=6cm，点P以2cm/s的速度沿A→C→E向终点E运动，同时点Q以3cm/s的速度从E开始，在线段EC上往返运动（即沿E→C→E→C→…运动），当点P到达终点时，P，Q同时停止运动.过P，Q分别作BD的垂线，垂足为M，N.设运动时间为t s，当以P，C，M为顶点的三角形与△QCN全等时，t的值为（）

A . 1或3 B . 1或 $\text{[math]}$ C . 1或 $\text{[math]}$ 或 $\text{[math]}$ D . 1或 $\text{[math]}$ 或5

答案解析收藏纠错 + 选题
6. (2021八上·长沙期中) 如图，在测量一个小口圆形容器的壁厚时，李师傅用“X型转动钳”按如图方法进行测量，其中O是AD、CB的中点，由三角形全等的知识可知只要测量A、B的距离，即得C、D的距离，便能计算出圆形容器的壁厚.请问李师傅得到△AOB≌△COD的依据是（）

A . SAS B . SSS C . ASA D . HL

答案解析收藏纠错 + 选题
7. (2021·大连模拟) 如图，将△ABC绕点A逆时针旋转得到 $\text{[math]}$ ，点C的对应点为点 $\text{[math]}$ ， $\text{[math]}$ 的延长线交BC于点D ，连接AD ．则下列说法错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . AD平分 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022七下·揭西月考) 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚可以放进一个等腰直角三角板（AC=BC ，　∠ACB=90°）点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为（）

A . 10cm B . 14cm C . 20cm D . 6cm

答案解析收藏纠错 + 选题
9. (2021八上·黄陂期末) 如图，工人师傅常用角尺平分一个任意角.做法如下：如图， $\text{[math]}$ 是一个任意角，在边 $\text{[math]}$ 上分别取 $\text{[math]}$ ，移动角尺，使角尺两边相同的刻度分别与 $\text{[math]}$ 重合.则过角尺顶点 $\text{[math]}$ 的射线 $\text{[math]}$ 便是 $\text{[math]}$ 的平分线，其依据是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八上·翁源月考) 如图，△OCA≌△OBD，AO＝3，CO＝2，则AB的长为（）

A . 1 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题

二、填空题

11. (2021八上·吉林期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2021八上·玉田期中) 如图，正方形ABCD的边长为2，延长BC到点E ，使 $\text{[math]}$ ，连接DE ．动点P从点A出发，以每秒1个单位的速度沿 $\text{[math]}$ 向终点D运动，设点P的运动时间为t秒，当 $\text{[math]}$ 与 $\text{[math]}$ 全等时，t的值为秒．

答案解析收藏纠错 + 选题
13. (2021七上·龙口期中) 如图，要测量水池宽AB ，可从点A出发在地面上画一条线段AC ，使AC⊥AB ，再从点C观测，在BA的延长线上测得一点D ，使∠ACD=∠ACB ，这时量得AD＝110m ，则水池宽AB的长度是m ．

答案解析收藏纠错 + 选题
14. (2021七上·龙口期中) 如图，方格中有四个相同的正方形，则∠1，∠2，∠3的度数之和是．

答案解析收藏纠错 + 选题
15. (2021八上·通州期末) 在新年联欢会上，老师设计了“你说我画”的游戏．游戏规则如下：甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形．已知乙同学说出的前两个条件是“ $\text{[math]}$ ， $\text{[math]}$ ”．现仅存下列三个条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ．为了甲同学画出形状和大小都确定的 $\text{[math]}$ ，乙同学可以选择的条件有：．（填写序号，写出所有正确答案）

答案解析收藏纠错 + 选题

三、解答题

16. (2023七下·凤翔期末) 如图1，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图2，伞圈D沿着伞柄AP滑动时，总有伞骨 $\text{[math]}$ ， $\text{[math]}$ ，从而使得伞柄AP始终平分同一平面内两条伞骨所成的 $\text{[math]}$ ．请你说明其中的理由．

答案解析收藏纠错 + 选题
17. (2022七下·武功期末) 如图，小明和小华住在同一个小区不同单元楼，他们想要测量小明家所在单元楼AB的高度，首先他们在两栋单元楼之间选定一点E，然后小华在自己家阳台C处测得E处的俯角为∠1，小明站在E处测得楼顶A的仰角为∠2，发现∠1与∠2互余，过点F作FG⊥AB于点G，已知BG＝1米，BE＝CD＝20米，BD＝58米，点B、E、D在一条直线上，AB⊥BD，FE⊥BD，CD⊥BD，试求单元楼AB的高．（注：BE＝FG，BG＝EF，∠1与∠3互余）

答案解析收藏纠错 + 选题
18. (2022七上·莱西期中) 王强同学用10块高度都是 $\text{[math]}$ 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板 $\text{[math]}$ ，点C在 $\text{[math]}$ 上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．

答案解析收藏纠错 + 选题
19. (2020八上·新乐期中) 如图， $\text{[math]}$ 两点分别位于一个假山的两端，小明想用绳子测量 $\text{[math]}$ 间的距离：现在地上取一个可以直接到达A点和B点的点C，连接 $\text{[math]}$ 并延长到点D，使 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长到点E，使 $\text{[math]}$ ；连接 $\text{[math]}$ 并测量出它的长度. $\text{[math]}$ ，求 $\text{[math]}$ 的长度.

答案解析收藏纠错 + 选题
20. (2020八上·右玉月考) 如图，A ， B两建筑物位于河的两岸，要测它们之间的距离，可以从B点出发在河岸上画一条射线BF ，在BF上截取BC＝CD ，过D作DE∥AB ，使E ， C ， A在同一直线上，则DE的长就是A ， B之间的距离，请你说明道理．

答案解析收藏纠错 + 选题
21. 如图：A、B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长．他叔叔帮他出了一个这样的主意：先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到E，使CD=AC；连接BC并延长到E，使CE=CB；连接DE并测量出DE=8m；
问题：DE=AB吗？AB的长度是多少？请说明理由．

答案解析收藏纠错 + 选题
22. 杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：如图，AB∥OH∥CD，相邻的平行线间的距离相等，AC，BD相交于O，OD⊥CD．垂足为D，已知AB=18米，请根据上述信息求标语CD的长度．

答案解析收藏纠错 + 选题
23. 如图，两根旗杆AC与BD相距12m，某人从B点沿AB走向A，一定时间后他到达点M，此时他仰望旗杆的顶点C和D，两次视线夹角为90°，且CM=DM．已知旗杆AC的高为3m，该人的运动速度为0.5m/s，求这个人走了多长时间？

答案解析收藏纠错 + 选题
24. (2017八下·罗山期末)
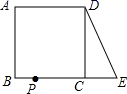
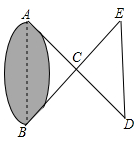
提出问题：如图1，将三角板放在正方形ABCD上，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交边DC与点E，求证：PB=PE
分析问题：学生甲：如图1，过点P作PM⊥BC，PN⊥CD，垂足分别为M，N通过证明两三角形全等，进而证明两条线段相等．
学生乙：连接DP，如图2，很容易证明PD=PB，然后再通过“等角对等边”证明PE=PD，就可以证明PB=PE了．
解决问题：请你选择上述一种方法给予证明．
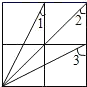
问题延伸：如图3，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交DC的延长线于点E，PB=PE还成立吗？若成立，请证明；若不成立，请说明理由．

答案解析收藏纠错 + 选题