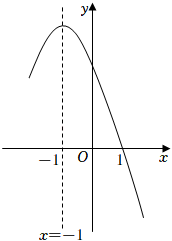15.
(2022九上·牟平期中)
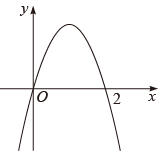
小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax
2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax
2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y
1),(﹣2,y
2),(3,y
3)均在二次函数图象上,则y
1<y
2<y
3;⑤3a+c<0,其中正确的结论有
.(填序号,多选、少选、错选都不得分)
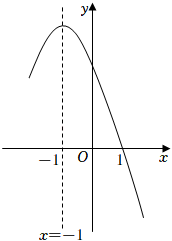
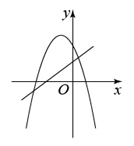 B .
B .  C .
C . 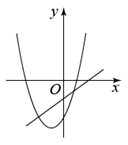 D .
D .