
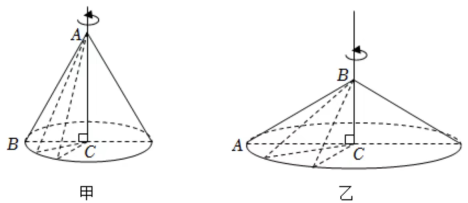
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗?请说明理由.
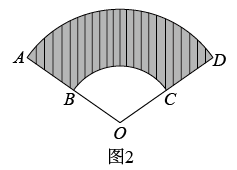
 问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为
问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形
, 圆锥底面是一个半径为r的圆.母线
在展开图上对应的半径
经过
的中点.
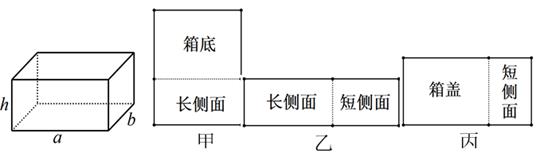
甲的面积;乙的面积;丙的面积.
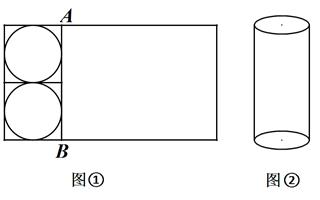
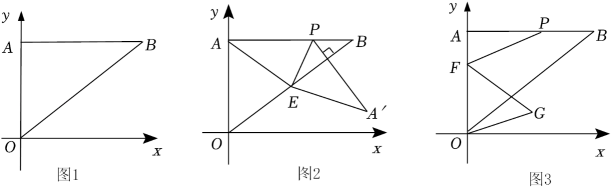


【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中 ,
,
.
【问题探究】
小昕同学将三角板 绕点
按顺时针方向旋转.