浙教版备考2023年中考数学一轮复习84.数据的收集与处理

更新时间：2023-01-09 浏览次数：73 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2024九上·中江期末) 下列说法中，正确的是（）

A . 调查某班45名学生的身高情况宜采用全面调查 B . “太阳东升西落”是不可能事件 C . 为了直观地介绍空气各成分的百分比，最适合使用的统计图是条形统计图 D . 任意投掷一枚质地均匀的硬币26次，出现正面朝上的次数一定是13次

答案解析收藏纠错 + 选题
2. (2023八上·霞山开学考) 垃圾分类利国利民，某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动，他们随机采访50名学生并作好记录．以下是排乱的统计步骤：
①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率；
②整理采访记录并绘制空矿泉水瓶投放频数分布表；
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比.
正确统计步骤的顺序应该是（）

A . ②→③→① B . ②→①→③ C . ③→①→② D . ③→②→①

答案解析收藏纠错 + 选题
3. (2024九下·新安模拟) 以下调查中，最适合采用抽样调查的是（）

A . 了解全国中学生的视力和用眼卫生情况 B . 了解全班 $\text{[math]}$ 名同学每天体育锻炼的时间 C . 学校招聘教师，对应聘人员进行面试 D . 为保证神舟十四号载人飞船成功发射，对其零部件进行检查

答案解析收藏纠错 + 选题
4. (2022七上·青州期中) 某校有3000名学生在线观看了“天宫课堂”第二课，并参加了关于“你最喜爱的太空实验”的问卷调查，从中抽取500名学生的调查情况进行统计分析，以下说法错误的是（）

A . 3000名学生的问卷调查情况是总体 B . 500名学生的问卷调查情况是样本 C . 500名学生是样本容量 D . 每一名学生的问卷调查情况是个体

答案解析收藏纠错 + 选题
5. (2022·衢州) 如图是某品牌运动服的S号，M号，L号，XL号的销售情况统计图，则厂家应生产最多的型号为（）

A . S号 B . M号 C . L号 D . XL号

答案解析收藏纠错 + 选题
6. (2022·福建) 2021年福建省的环境空气质量达标天数位居全国前列，下图是福建省10个地区环境空气质量综合指数统计图.

综合指数越小，表示环境空气质量越好.依据综合指数，从图中可知环境空气质量最好的地区是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·台湾) 某国主计处调查2017年该国所有受雇员工的年薪资料，并公布调查结果如图的直方图所示.

已知总调查人数为750万人，根据图中信息计算，该国受雇员工年薪低于平均数的人数占总调查人数的百分率为下列何者？（）

A . 6% B . 50% C . 68% D . 73%

答案解析收藏纠错 + 选题
8. (2022·徐州) 我国近十年的人口出生率及人口死亡率如图所示．
已知人口自然增长率=人口出生率—人口死亡率，下列判断错误的是（）

A . 与2012年相比，2021年的人口出生率下降了近一半 B . 近十年的人口死亡率基本稳定 C . 近五年的人口总数持续下降 D . 近五年的人口自然增长率持续下降

答案解析收藏纠错 + 选题
9. (2021·徐州) 第七次全国人民普查的部分结果如图所示.

根据该统计图，下列判断错误的是（）

A . 徐州0－14岁人口比重高于全国 B . 徐州15－59岁人口比重低于江苏 C . 徐州60岁以上人口比重高于全国 D . 徐州60岁以上人口比重高于江苏

答案解析收藏纠错 + 选题
10. (2022·聊城) “俭以养德”是中华民族的优秀传统，时代中学为了对全校学生零花钱的使用进行符合题意引导，随机抽取50名学生，对他们一周的零花钱数额进行了统计，并根据调查结果绘制了不完整的频数分布表和扇形统计图，如图所示：
组别
零花钱数额 $\text{[math]}$ /元
频数
一
$\text{[math]}$
二
$\text{[math]}$
12
三
$\text{[math]}$
15
四
$\text{[math]}$
$\text{[math]}$
五
$\text{[math]}$
5
关于这次调查，下列说法正确的是（）

A . 总体为50名学生一周的零花钱数额 B . 五组对应扇形的圆心角度数为36° C . 在这次调查中，四组的频数为6 D . 若该校共有学生1500人，则估计该校零花钱数额不超过20元的人数约为1200人

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2024七下·汕头期末) 某班按课外阅读时间将学生分为3组，第1、2组的频率分别为0.2、0.5，则第3组的频率是 .

答案解析收藏纠错 + 选题
12. (2022七上·山西期末) 想要了解本周天气的变化情况，最适合采用统计图(填“扇形”、“折线”或“条形”)．

答案解析收藏纠错 + 选题
13. (2024九下·成都月考) 近年来，洞庭湖区环境保护效果显著，南迁的候鸟种群越来越多．为了解南迁到该区域某湿地的A种候鸟的情况，从中捕捉40只，戴上识别卡并放回；经过一段时间后观察发现，200只A种候鸟中有10只佩有识别卡，由此估计该湿地约有只A种候鸟．

答案解析收藏纠错 + 选题

14. (2023七上·桥西期末) $\text{[math]}$ 市安排若干名医护工作人员援助某地新冠疫情防控工作，人员结构统计如下表：

人员	领队	心理医生	专业医生	专业护士
占总人数的百分比	4%		$\text{[math]}$	56%

则该批医护工作人员中“专业医生”占总人数的百分比为.

答案解析收藏纠错 + 选题

15. 为制订某区七年级学生校服的生产计划，有关部门需要了解七年级男生的身高情况.现有三种调查方案；
①测量该区各学校男子篮球队﹑排球队中七年级学生的身高；②查阅外区各校七年级男生身高的统计资料；③在该区的城区和农村均任选几所学校，测量这几所学校七年级男生的身高.你认为上述调查方案中比较合适的是.(只填写序号)

答案解析收藏纠错 + 选题
16. (2020八上·长子期末) 某校八年级（1）班团支部为了让同学们进一步了解中国科技的发展，给班上同学布置了一项课外作业，从选出的以下五个内容中任选一个内容进行手抄报的制作．A．“北斗卫星”；B．“5G时代”；C．“智轨快运系统”；D．“东风快递”；E．“高铁”．统计同学们所选内容的频数，绘制如图所示的折线统计图，则选“5G时代”的频率为．

答案解析收藏纠错 + 选题

三、解答题（共8题，共72分）

17. (2022·淮安) 某校计划成立学生体育社团，为了解学生对不同体育项目的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个体育项目”问卷调查，规定每人必须并且只能在“篮球”“足球”“乒乓球”“健美操”“跑步”五个项目中选择一项，并根据统计结果绘制了两幅不完整的统计图.
请解答下列问题：
1. （1）在这次调查中，该校一共抽样调查了名学生，扇形统计图中“跑步”项目所对应的扇形圆心角的度数是°；
2. （2）请补全条形统计图；
3. （3）若该校共有1200名学生，试估计该校学生中最喜爱“篮球”项目的人数.
答案解析收藏纠错 + 选题
18. (2022·衢州) 【新知学习】在气象学上，“入夏”由两种平均气温与22℃比较来判断：
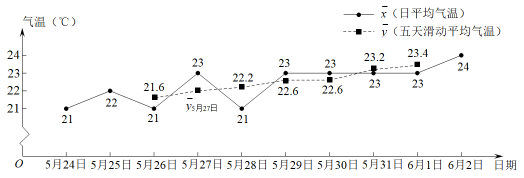
衢州市2021年5月5日~5月14日的两种平均气温统计表（单位：℃）

注：“五天滑动平均气温”指某一天及其前后各两天的日平均气温的平均数，如：

$\text{[math]}$ (℃)．

已知2021年的 $\text{[math]}$ 从5月8日起首次连续五天大于或等于22℃，而 $\text{[math]}$ 对应着 $\text{[math]}$ ~ $\text{[math]}$ ，其中第一个大于或等于22℃的是 $\text{[math]}$ ，则5月7日即为我市2021年的“入夏日”．

【新知应用】已知我市2022年的“入夏日”为下图中的某一天，请根据信息解决问题：

衢州市2022年5月24日~6月2日的两种平均气温折线统计图
1. （1）求2022年的 $\text{[math]}$ .
2. （2）写出从哪天开始，图中的 $\text{[math]}$ 连续五天都大于或等于22℃．并判断今年的“入夏日”．
3. （3）某媒体报道：“夏天姗姗来迟，衢州2022年的春天比去年长．”你认为这样的说法正确吗？为什么？（我市2021年和2022年的入春时间分别是2月1日和2月27日）
答案解析收藏纠错 + 选题

19. (2022·镇江) 某地交警在一个路口对某个时段来往的车辆的车速进行监测，统计数据如下表：

车速（ $\text{[math]}$ ）	40	41	42	43	44	45
频数	6	8	15	$\text{[math]}$	3	2

其中车速为40、43（单位： $\text{[math]}$ ）的车辆数分别占监测的车辆总数的12%、32%．

（1）求出表格中 $\text{[math]}$ 的值；
（2）如果一辆汽车行驶的车速不超过 $\text{[math]}$ 的10%，就认定这辆车是安全行驶．若一年内在该时段通过此路口的车辆有20000辆，试估计其中安全行驶的车辆数．

答案解析收藏纠错 + 选题

20. (2022·襄阳) 在“双减”背景下，某区教育部门想了解该区A，B两所学校九年级各500名学生的课后书面作业时长情况，从这两所学校分别随机抽取50名九年级学生的课后书面作业时长数据（保留整数），整理分析过程如下：

【收集数据】A学校50名九年级学生中，课后书面作业时长在70.5≤x＜80.5组的具体数据如下：

74，72，72，73，74，75，75，75，75，

75，75，76，76，76，77，77，78，80

【整理数据】不完整的两所学校的频数分布表如下，不完整的A学校频数分布直方图如图所示：

组别	50.5≤x＜60.5	60.5≤x＜70.5	70.5≤x＜80.5	80.5≤x＜90.5	90.5≤x＜100.5
A学校	5	15	x	8	4
B学校	7	10	12	17	4

【分析数据】两组数据的平均数、众数、中位数、方差如下表：

特征数	平均数	众数	中位数	方差
A学校	74	75	y	127.36
B学校	74	85	73	144.12

根据以上信息，回答下列问题：

（1）本次调查是调查（选填“抽样”或“全面”）；
（2）统计表中，x＝，y＝；
（3）补全频数分布直方图；
（4）在这次调查中，课后书面作业时长波动较小的是学校（选填“A”或“B”）；
（5）按规定，九年级学生每天课后书面作业时长不得超过90分钟，估计两所学校1000名学生中，能在90分钟内（包括90分钟）完成当日课后书面作业的学生共有人．

答案解析收藏纠错 + 选题

21. (2022·安顺) 国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出，要加强中小学生作业、睡眠、手机、读物、体质管理．某校数学社团成员采用随机抽样的方法，抽取了七年级部分学生，对他们一周内平均每天的睡眠时间 $\text{[math]}$ （单位：小时）进行了调查，将数据整理后得到下列不完整的统计表：

睡眠时间	频数	频率
$\text{[math]}$	3	0.06
$\text{[math]}$	$\text{[math]}$	0.16
$\text{[math]}$	10	0.20
$\text{[math]}$	24	$\text{[math]}$
$\text{[math]}$	5	0.10

请根据统计表中的信息回答下列问题．

（1） $\text{[math]}$ ， $\text{[math]}$ ；
（2）请估计该校600名七年级学生中平均每天的睡眠时间不足9小时的人数；
（3）研究表明，初中生每天睡眠时间低于9小时，会影响学习效率．请你根据以上调查统计结果，向学校提出一条合理化的建议．

答案解析收藏纠错 + 选题

22. (2022·丹东) 为了解学生一周劳动情况，我市某校随机调查了部分学生的一周累计劳动时间，将他们一周累计劳动时间t（单位：小时）划分为A：t＜2，B：2≤t＜3，C：3≤t＜4，D：t≥4四个组，并将调查结果绘制成如图所示的两幅不完整的统计图，根据图中所给信息解答下列问题：
1. （1）这次抽样调查共抽取人，条形统计图中的m＝；
2. （2）在扇形统计图中，求B组所在扇形圆心角的度数，并将条形统计图补充完整；
3. （3）已知该校有960名学生，根据调查结果，请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人？
4. （4）学校准备从一周累计劳动时间较长的两男两女四名学生中，随机抽取两名学生为全校学生介绍劳动体会，请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率．
答案解析收藏纠错 + 选题

23. (2022·鄂尔多斯) 为了调查九年级学生寒假期间平均每天观看冬奥会时长情况，随机抽取部分学生进行调查，根据收集的数据绘制了如图所示两幅不完整的统计图

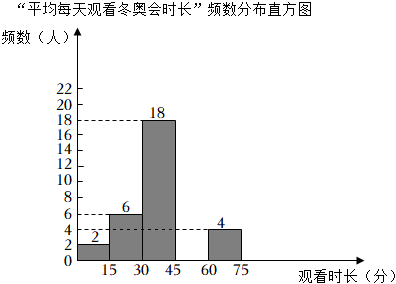
“平均每天观看冬奥会时长”频数分布表

观看时长（分）	频数（人）	频率
0＜x≤15	2	0.05
15＜x≤30	6	0.15
30＜x≤45	18	a
45＜x≤60		0.25
60＜x≤75	4	0.1

（1）频数分布表中，a＝ ▲ ，请将频数分布直方图补充完整；
（2）九年级共有520名学生，请你根据频数分布表，估计九年级学生平均每天观看冬奥会时长超过60分钟的有人；
（3）校学生会拟在甲、乙、丙、丁四名同学中，随机抽取两名同学做“我与冬奥”主题演讲，请用树状图或列表法求恰好抽到甲、乙两名同学的概率．

答案解析收藏纠错 + 选题

24. 为了解学生的身高情况，抽测了某校17岁的50名男生的身高，将数据分成7组，列出了相应的频数表(部分未列出)如下.

某校50名17岁男生身高的频数表

分组(m)	频数	频率
1.565～1.595	2	0.04
1.595~1.625	______	______
1.625~1.655	6	0.12
1.655~1.685	11	0.22
1.685~1.715	______	0.34
1.715～1.745	6	______
1.745~1.775	4	0.08
合计	50	1

请回答下列问题.

（1）请将上述频数表填写完整；
（2）估计这所学校17岁男生中，身高不低于1.655 m且不高于1.715 m的学生所占的百分比；
（3）该校17岁男生中，身高在哪个范围内的频数最多？如果该校17岁男生共有350名，那么在这个身高范围内的大约有多少人？

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙教版备考2023年中考数学一轮复习84.数据的收集与处理

副标题：

*注意事项：

浙教版备考2023年中考数学一轮复习84.数据的收集与处理

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

组别	零花钱数额 $\text{[math]}$ /元	频数
一	$\text{[math]}$
二	$\text{[math]}$	12
三	$\text{[math]}$	15
四	$\text{[math]}$	$\text{[math]}$
五	$\text{[math]}$	5